Published online by Cambridge University Press: 24 October 2008
Verblunsky has recently proved the following theorem:
Theorem A. Suppose that
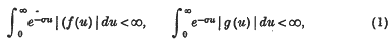
for every positive σ. Write
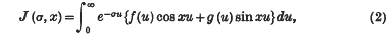
and suppose that J (σ, x) is bounded in σ, x for σ > 0 and all x. Then

exists almost everywhere, and
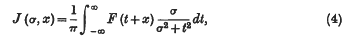
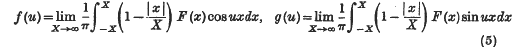
almost everywhere.
page 382 note * Verblunsky, S., “Trigonometric integrals and harmonic functions”, Proc. London Math. Soc. (2), 38 (1934), 1–48 (19)Google Scholar. Verblunsky does not state the hypothesis (1) explicitly in the enunciation of his theorem, but it is understood throughout the paper. It is employed in the proof of this particular theorem on p. 20.
page 382 note † Offord, A. C., “On Fourier transforms”, Proc. London Math. Soc. (2), 38 (1934), 197–216Google Scholar, and “On Fourier transforms (II)”, ibid., in the press. We refer to these papers as I and II respectively.
page 385 note * See, for example, Hardy, and Riesz, , The general theory of Dirichlet's series, p. 29Google Scholar. The proofs for series and integrals are the same.