Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1926.
The mechanism of ciliary movement. —V. The effect ions the duration of beat.
Proceedings of the Royal Society of London. Series B, Containing Papers of a Biological Character,
Vol. 99,
Issue. 698,
p.
398.
1926.
Croonian Lecture:—The laws of muscular motion.
Proceedings of the Royal Society of London. Series B, Containing Papers of a Biological Character,
Vol. 100,
Issue. 701,
p.
87.
Gray, Brayton
1985.
On Toda's fibrations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 97,
Issue. 2,
p.
289.
Gray, Brayton
1988.
On the iterated suspension.
Topology,
Vol. 27,
Issue. 3,
p.
301.
Thompson, Robert D.
1989.
Unstable 𝑣₁-periodic homotopy groups of a Moore space.
Proceedings of the American Mathematical Society,
Vol. 107,
Issue. 3,
p.
833.
Gray, Brayton
1989.
Algebraic Topology.
Vol. 1370,
Issue. ,
p.
150.
Thompson, Robert D.
1990.
The 𝑣₁-periodic homotopy groups of an unstable sphere at odd primes.
Transactions of the American Mathematical Society,
Vol. 319,
Issue. 2,
p.
535.
Gray, Brayton
1993.
𝐸𝐻𝑃 spectra and periodicity. I. Geometric constructions.
Transactions of the American Mathematical Society,
Vol. 340,
Issue. 2,
p.
595.
Mahowald, Mark E.
and
Ravenel, Douglas C.
1993.
The root invariant in homotopy theory.
Topology,
Vol. 32,
Issue. 4,
p.
865.
Hemmi, Yutaka
and
Kawamoto, Yusuke
1996.
Decomposability of the mod $p$ Whitehead element.
Hiroshima Mathematical Journal,
Vol. 26,
Issue. 3,
Imaoka, Mitsunori
and
Kawamoto, Yusuke
1997.
Symmetricity of the Whitehead element.
Hiroshima Mathematical Journal,
Vol. 27,
Issue. 2,
Scheerer, Hans
Stanley, Donald
and
Tanré, Daniel
2002.
Fibrewise construction applied to Lusternik-Schnirelmann category.
Israel Journal of Mathematics,
Vol. 131,
Issue. 1,
p.
333.
Bendersky, Martin
and
Davis, Donald M.
2003.
Compositions in the ν1 -periodic homotopy groups of spheres.
Forum Mathematicum,
Vol. 15,
Issue. 2,
Gray, Brayton
2005.
On decompositions in homotopy theory.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 8,
p.
3305.
Grbić, Jelena
Harper, John
Mimura, Mamoru
Theriault, Stephen
and
Wu, Jie
2013.
Rank p − 1 mod-p H-spaces.
Israel Journal of Mathematics,
Vol. 194,
Issue. 2,
p.
641.
Assimos, Renan
Savas-Halilaj, Andreas
and
Smoczyk, Knut
2023.
Graphical mean curvature flow with bounded bi-Ricci curvature.
Calculus of Variations and Partial Differential Equations,
Vol. 62,
Issue. 1,
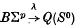 .All our constructions are made in BΣp and transferred over.
.All our constructions are made in BΣp and transferred over.