Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T04:58:16.827Z Has data issue: false hasContentIssue false
  • English
  • Français

The Wave Mechanics of an Atom with a non-Coulomb Central Field. Part III. Term Values and Intensities in Series in Optical Spectra

Published online by Cambridge University Press:  24 October 2008

D. R. Hartree
D. R. Hartree
Affiliation:
Christ's College
Get access Rights & Permissions [Opens in a new window]

Extract

In two recent papers the writer has given an account of a practical method of finding the characteristic values and functions of Schrödinger's wave equations for a given non-Coulomb central field. For terms of optical spectra the method is effectively the following. We take the wave equation in the form

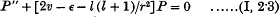
and require the values of ɛ for the solutions which are zero at the origin and at r = ∞. We consider the result of integrating this equation outwards from P = 0 at r = 0 to a radius r0 at which the deviation from a Coulomb field is negligible, and inwards from P = 0 at r = ∞ to the same radius, with a given value of ɛ; the characteristic values are those values for which these two solutions join smoothly on to one another, i.e. for which they have the same value of η = −P′/P at this radius. For a given ɛ, the solution zero at the origin depends on the particular atom; the solution zero at infinity can be expressed in a form independent of any particular atom.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 24 , Issue 3 , July 1928 , pp. 426 - 437
Copyright
Copyright © Cambridge Philosophical Society 1928

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Proc. Camb. Phil. Soc. vol. 24, pp. 89, 111 (1928). These papers will be referred to as I and II. The same notation will be used here as in those papers, with the exception that the effective quantum number will be written n instead of n*.CrossRefGoogle Scholar

† Each solution contains an arbitrary multiplying constant, hence the form of the condition for the solutions to fit.Google Scholar

‡ This solution cannot be treated as a variation on the solution for ɛ=0, as for any ɛ, however small, ɛ is the leading term in P″/P for r sufficiently large, and the solution for such values of r for any ɛ ≠ 0 is essentially different from that for ɛ = 0.Google Scholar

* Eddington, A. S., Nature, vol. 120, p. 117 (1927).CrossRefGoogle Scholar

† Sugiura, Y., Phil. Mag. Ser. 7, vol. 4, p. 498 (1927).CrossRefGoogle Scholar

‡ See Whittaker, E. T. and Watson, G. N., Modern Analysis, ch. 16.Google Scholar

§ Op. cit. § 16·12.Google Scholar

‖ Op. cit. § 16·1.Google Scholar

Op. cit. § 16·41.Google Scholar

* See, for example, Piaggio, H. T. H., Differential Equations, § 98.Google Scholar

* Cf. Whittaker, and Watson, , op. cit. ch. 12. Writing γ for Euler's Constant, we have the special valuesψ(1)=−γ, (n integral).Google Scholar

† Cf. Whittaker, and Watson, , op. cit. § 12–33.Google Scholar

* See Jahnke, E. and Emde, F., Funktionentafeln, p. 166. [Put β = 2, γ = ½, p = 2l + 1 in the second equation of § 13.]Google Scholar

† Watson, G. N., Treatise on Bessel Functions, § 3·52 (3), and § 3·54 (2).Google Scholar

* Op. cit. § 16·41.Google Scholar

* Dashes denote differentiation with respect to r.Google Scholar

* See Whittaker, and Watson, , op. cit. § 16·3.Google Scholar

* The square of the matrix amplitude for the transition is [cf. Sugiura, loc. cit. equation (4)] multiplied by an absolute constant and by a factor depending on lA and lB, arising from the dependence of the wave functions on direction of the radius r. The factor v 4 arises from the relation between doublet amplitude and intensity of emitted radiation.Google Scholar