No CrossRef data available.
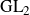 $\textrm{GL}_2$ L-functions
$\textrm{GL}_2$ L-functionsPublished online by Cambridge University Press: 28 December 2022
We prove an analogue of Selberg’s zero density estimate for
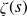 $\zeta(s)$
that holds for any
$\zeta(s)$
that holds for any
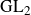 $\textrm{GL}_2$
L-function. We use this estimate to study the distribution of the vector of fractional parts of
$\textrm{GL}_2$
L-function. We use this estimate to study the distribution of the vector of fractional parts of
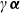 $\gamma\boldsymbol{\alpha}$
, where
$\gamma\boldsymbol{\alpha}$
, where
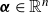 $\boldsymbol{\alpha}\in\mathbb{R}^n$
is fixed and
$\boldsymbol{\alpha}\in\mathbb{R}^n$
is fixed and
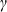 $\gamma$
varies over the imaginary parts of the nontrivial zeros of a
$\gamma$
varies over the imaginary parts of the nontrivial zeros of a
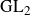 $\textrm{GL}_2$
L-function.
$\textrm{GL}_2$
L-function.