Published online by Cambridge University Press: 24 October 2008
Let ψ be a distribution function on [−1,1] from the Szegö-class, which contains in particular all Jacobi weights, and let (pn) be the monic polynomials orthogonal with respect to dψ. Let m(n)∈ℕ, n∈ℕ, be non-decreasing with limn → ∞ (n − m(n)) = ∞, l(n)∈ℕ with 0 ≤ l(n) ≤ m(n), and μj, n ∈ℝ for j = 0, …, m(n), n∈ℕ. It is shown that for each sufficiently large n, 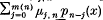 has n−l(n) simple zeros in (−1, 1)and l(n) zeros in ℂ\[−1,1] if for n ≥ n0,
has n−l(n) simple zeros in (−1, 1)and l(n) zeros in ℂ\[−1,1] if for n ≥ n0, 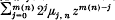 has m(n) − l(n) zeros in the disc |z| ≤ r < 1, l(n) zeros outside of the disc |z| ≥ R > 1 and
has m(n) − l(n) zeros in the disc |z| ≤ r < 1, l(n) zeros outside of the disc |z| ≥ R > 1 and 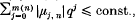 where q > 2 max {r, 1/R}. If m(n) is constant for n ≥ n0 then the statement holds even for such polynomials (pn) orthogonal with respect to a distribution dψ satisfying the weak assumption ψ′ > 0 a.e. on [−1, 1]. For linear combinations of polynomials orthogonal on the unit circle corresponding results are derived.
where q > 2 max {r, 1/R}. If m(n) is constant for n ≥ n0 then the statement holds even for such polynomials (pn) orthogonal with respect to a distribution dψ satisfying the weak assumption ψ′ > 0 a.e. on [−1, 1]. For linear combinations of polynomials orthogonal on the unit circle corresponding results are derived.