Porte (1), p. 117, conjectures that the positive implicational propositional calculus has no finite characteristic matrix. The proof of this conjecture is a straightforward modification of Gödel's proof (2) that the intuitionistic propositional calculus has no finite characteristic matrix (see e.g. Church(3), ex. 26.12). Writing (A ∨ B) for ((A ⊃ B) ⊃ B) and Xij for (pj ⊃ pi) (i, j = 1,2,…), we define, for n > l, the formula

where the terms associate to the left. Since provable formulae take the value n for all systems of values of the variables in the matrix {1,…,n} where x ⊃ y is n when x ≤ y and y otherwise, whereas Gn takes the value n − 1 for the system of values pi = i (i = 1,…,n), it follows that Gn is not provable. On the other hand, since A ⊢ A ∨ B and B ⊢ A ∨ B, it is easily seen that is provable whenever r ≠ s (r, s = 1,…,n). The result follows from these two remarks.

Kruskal's theorem for obtaining a minimal (maximal) spanning tree of a graph is shown to be a special case of a more general theorem for matroid spaces in which each element of the matroid has an associated weight. Since any finite subset of a vector space can be regarded as a matroid space this theorem gives an easy method of selecting a linearly independent set of vectors of minimal (maximal) weight.

In his discussion (3) of automorphisms of finite simple linear groups, Steinberg shows that the group denoted by B2(K) admits graph automorphisms when K is a perfect field of characteristic 2. The group B2(K) is identified in (2) as the symplectic group Sp4(K) when K is finite and of characteristic 2, and it is the object of this note to give, by means of this identification, an explicit description of the graph automorphisms of B2(2n).

Let p be a prime and n ≥ 3. Then there is a simply connected CW-complex, , unique up to homotopy type, such that

Let X be a CW-complex. Write , the group of pointed homotopy classes of pointed maps from to X. The group structure derives from the fact that, under the restriction on n, is a suspension.

Since Thom first introduced the notion of the ‘dual’ of a Steenrod square, in (12), it has become apparent that calculation with such duals in the cohomology of, say, a simplicial complex X will often yield information about the impossibility of embedding X in Sn, for certain values of n. For example, the celebrated theorem that cannot be embedded in can easily be proved in this way. In this paper, we seek to generalize this method to any pair of extraordinary cohomology theories h* and k*, and natural stable cohomology operation θ: h* → k*. We show in section 3 that a simplicial embeddingf: X → Sn gives rise via the Alexander duality isomorphism to a homology operation

which is independent of n, the particular embedding f, and even the particular triangulations of X and Sn. If h* and k* are multiplicative cohomology theories, there are Kronecker products

if h0(S0) = k0(S0) = G, a field, and the Kronecker products make h*, h* and k*, k* into dual vector spaces over G, then can be turned into a cohomology operation c(θ): k*(X)→h*(X), by using this duality. This is certainly true if h* = k* = H*(;Zp), p prime, and in this case we have the original situation considered by Thom, who showed, for example, that

Given any triangulation of a topological n-cell, In, there is an integer k such that the kth barycentric subdivision of the triangulation is simplicially collapsible (3). In the following, we show that given any integer k, we can construct a triangulation of an n-cell, n > 2, whose kth barycentric subdivision is not simplicially collapsible.

Gel'fand and Šilov(1) have introduced the concept of compatibility of norms on a vector space, defining two norms to be compatible if each sequence which is Cauchy with respect to both norms and converges to zero with respect to one norm, also converges to zero with respect to the other. They have found it convenient to build up their exposition of spaces of generalized functions (2) by developing the theory of locally convex spaces whose topology can be defined by a countable set of pairwise compatible norms. The author (3) has examined the properties of locally convex spaces which have been topologized by making a set of linear mappings into locally convex spaces continuous, and has shown that if this method is applied to a set of closed operators on Hilbert space, then the resulting spaces have topologies generated by a set of pairwise compatible norms. The purpose of this paper is to generalize this result by putting it in its natural context as a theorem on uniformities which have been defined by making a closed set of mappings uniformly continuous. The closed mappings of the title are mappings with closed graph.

Alexander's theorem (5) states that a topological space is compact if there is a sub-base, , for its closed sets such that every subclass of with the finite intersection property has a non-empty intersection. An analysis and extension of this is given here which has applications, inter alia, to problems concerning real-compactness (2).

In this paper I investigate the completed projective tensor product of two perfect Riesz spaces, and show how a natural order structure on this renders it also a perfect Riesz space. Sections 7–14 contain interesting order-topological properties of this tensor product. Finally, section 15 describes how the tensor product of function spaces may be represented as a function space, in the manner of (1 b).

Let be a real algebra which is also a Banach space. Then is called a partially ordered Banach algebra if there is specified a non-empty subset of , called the positive cone, such that

and

(A 5) is 1-normal and closed. (We recall that is said to be 1-normal if

Suppose that

belongs to L2( − π, π). If most of the coefficients vanish then f (x) cannot be too small in a certain interval without being small generally. More precisely Ingham ((2), Theorem 1) has proved the following

THEOREM A. Suppose that f (x) is given by (1·1) and that an = 0, except for a sequence n = nν, where nν+1 − nν ≥ C. Then given ∈ > 0 there exists a constant A (∈), such that we have for any real x1

We use J(a, b) to denote a Jordan curve of positive two-dimensional measure in the plane, with end-points a and b. If υ is a point of J(a, b), we define the right lower arc density at υ by

where J( υ, υ′) is the largest arc, whose left-end point is υ, which is contained in the disc c(υ, r).

1. Suppose that f is a function analytic on a region G in complex n-space Cn, and that f(m)(w(m)) = 0 for each m = (m1, m2,…, mn), mi = 0, 1, 2,…, where

We will here prove the following special case of an (unpublished) conjecture for a polynomial of degree ndue to L. Ilieff:

Theorem. If all zeros of the cubic polynomial p3(z) lie in |z| ≤ 1, then at least one zero of p3′(z) lies in or on the boundary of a circle of radius unity around each zero of p′3(z).

This paper is concerned with estimates of the coefficients Cn for normalized polynomials, inverse to univalent functions in the unit disc, i.e. univalent polynomials of the form

considered in the largest domain D such that 0 ∈ D and |pn(w)| < 1 for w ∈ D; this domain will be denoted by . Polynomials of the type (1) have been introduced by Charzyński in (1), where it was proved among other results that the domain is simply connected.

In a recent paper Ragab and Simary (6) have deduced some integrals involving the products of generalized Whittaker functions. We feel that some of the integrals are not correctly evaluated. Indeed the integral (2) should be symmetrical in α and β, as we see by changing the variables by s = − t in the integral, while it is not symmetrical. A similar remark will follow in the case of the integrals (3) and (6).

An identity for a rational function is used, in conjunction with generating functions for a certain class of polynomials, to derive infinite sets of identities for these polynomials. Identities are given for the polynomials of Legendre, Gegenbauer, Hermite, Tchebycheff and L. Carlitz. A novel type of classification for these polynomials is indicated. Next, infinite sequences of identities for various Bessel functions and for power functions are derived. New identities for trigonometric functions are also given, as well as brief miscellanea on: functions resembling Dirac's delta function, integral transforms and a functional equation.

Non-linear integral equations and relations, whose nuclei in all cases is the ‘potential’ Green's function, satisfied by Lamé polynomials and Lamé functions of the second kind are discussed. For these functions certain techniques of analysis are described and these find their natural generalization in ellipsoidal wave-function theory. Here similar integral equations are constructed for ellipsoidal wave functions of the first and third kinds, the nucleus in each case now being the ‘free space’ Green's function. The presence of ellipsoidal wave functions of the second kind is noted for the first time. Certain possible generalizations of the techniques and ideas involved in this paper are also discussed.

We consider in this paper the solution behaviour as s → 0 of the equation

where the primes indicate differentiation with respect to s, and a, b, c are constants.

In a simple homogeneous birth-and-death process with λ and μ as the constant birth and death rates respectively, let X(t) denote the population size at time t, Z(t) the number of deaths and N(t) the number of events (births and deaths combined) occurring during (0, t). Also let 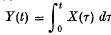. The results obtained include the following:

(a) An explicit formula for the characteristic quasi-probability generating function of the joint distribution of X(t), Y(t) and Z(t).

(b) Let X(0) = 1. It is shown that, if t → ∞ while λ ≤ μ, N(t) ↑ N a.s., where N takes only positive odd integral values. If λ > μ, then P[N(t) ↑ ∞] = 1 − μ/λ. Given that N(t)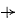∞, the limiting distribution of N(t) is similar to that of N. It was reported earlier (Puri (11)), that the limiting distribution of Y(t) is a weighted average of certain chi-square distributions. It is now found that these weights are nothing but the probabilities P[N = 2k + 1] (k = 0, 1,…).

(c) Let λ = μ, and MXω), MYω and MZω be defined as in (36), then as

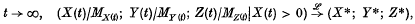
where the c.f. of (X*; Y*; Z*) is given by (38).

(d) Exact expressions for the p.d.f. of Y(t) are derived for the cases (i) λ = 0, μ > 0, (ii) λ > 0, μ = 0. For the case (iii) λ gt; 0, μ > 0, since the complete expression is complicated, only the procedure of derivation is indicated.

(e) Finally, it is shown that the regressions of Y(t) and of Z(t) on X(t) are linear for X(t) ≥ 1.