For r ∈ [0, 1] let μr be the Bernoulli measure on the Cantor set given as the infinite power of the measure on {0, 1} with weights r and 1 − r. For r, s ∈ [0, 1] it is known that the measure μr is continuously reducible to μs (that is, there is a continuous map sending μr to μs) if and only if s can be written as a certain kind of polynomial in r; in this case s is said to be binomially reducible to r. In this paper we answer in the negative the following question posed by Mauldin:
Is it true that the product measures μrand μsare homeomorphic if and only if each is a continuous image of the other, or, equivalently, each of the numbersrandsis binomially reducible to the other?
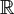 )
)
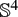 with zero Gauss–Kronecker curvature
with zero Gauss–Kronecker curvature
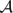 -simple map-germs from
-simple map-germs from 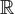 n to
n to 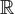 2n
2n