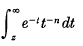Let α be a prime element of the ring of integers of an algebraic number field, R. Mr C. Sudler verbally raised the question as to how many prime ideal factors α can have. This is equivalent to a problem on the group of ideal classes of R, as we now show. If there is a prime α = p1p2 … Pk, where the prime ideal pi, is in the ideal class Pi, then P1P2…Pk equals the identity class, but no subproduct has this property. The converse holds since every ideal class contains prime ideals. So the problem is equivalent to one on finite Abelian groups, which we now write additively.

In (6), Kiang gives an example of a simply connected (closed) region D in 3-space R3, bounded by a smooth 2-sphere ∂D, whose (harmonic) Green's function Γ has a critical point for any choice of pole p ∈ Int D—contrary to the analogous 2-dimensional situation. It is not known whether any position of p exists, for which Γ is non-degenerate in the sense of Morse theory; however, we show here the following result.

In a previous paper (3) one of us reported an expansion for the exponential integral

in terms of Bessel functions. In this note, we shall obtain the more general formula

where n is any positive integer, γ is Euler's constant and

It reduces to that in (3) when n = 1.

In an earlier paper (1) the idea of a c-homeomorphism on a 2-manifold was introduced; it can be described in the following way. Let the 2-manifold M contain an annulus, A, one of the boundary components of which is a simple closed curve c. There is a homeomorphism of A to itself, fixed on the boundary of A, which sends radial arcs onto arcs which spiral once around A (see Fig. 1). This can be extended to

a homeomorphism of M to itself, by the identity on M — A. Intuitively this homeomorphism can be thought of as the process of cutting M along c, twisting one of the now free ends, and then glueing together again. The c-homeomorphism has, in fact, only been defined up to isotopy, but as we shall only be considering homeomorphisms up to isotopy, this is sufficient. It was shown in (1) that any orientation preserving homeomorphism of a closed orientable 2-manifold can be expressed as a product of c-homeomorphisms. In that case, a c-homeomorphism could be associated with any simple closed path on such a manifold, but on a non-orientable 2-manifold a c-homeomorphism can only be associated with a simple closed orientation preserving path. It is this fact that invalidates many of the lemmas of (1) if they are regarded as applying to the non-orientable case. The purpose of this paper is to show that (Theorem 1) c-homeomorphisms do not generate the group of all homeomorphisms of a closed nonorientable 2-manifold, but that if another elementary type of homeomorphism, the Y-homeomorphism, is introduced, then c- and Y-homeomorphisms together do generate this group (Theorem 2). This result leads to a discussion of non-orientable 3-manifolds, to a result analogous to that obtained for orientable 3-manifolds in (1), and to a new proof of the fact that any 3-manifold bounds a 4-manifold. Throughout this paper all manifolds will be considered as possessing an underlying combinatorial structure, all paths will be polygonal with respect to some subdivision of the manifold containing them, and all homeomorphisms and isotopies will be piecewise linear.

It was remarked in (1) that many of the results valid for compact (this term is taken to imply Hausdorff) semigroups with jointly continuous multiplication also hold if the multiplication is only separately continuous. It is the purpose of this note to show that this is true of the structure theorem for compact simple semigroups. Any unsubstantiated facts about semigroups which we use may be found in the second section of (1) (the results given there do not depend on the assumption that a semigroup should contain an identity).

1. The purpose of this note is to prove a result which includes certain classical theorems generally thought of as being unconnected; in explicit terms, a result about the Fourier series of a periodic Lebesgue-integrable function showing that the series is summable at a point by a Nörlund method (N, pn) defined as usual ((2), p. 64) if pn ↓ 0, Σpn = ∞ and the point is in a certain subset of the Lebesgue set. More precisely, the purpose is to prove Theorem I on the Nörlund summability of Fourier series and to derive from it the well-known Theorems A, B which follow and the recent extension of Theorem A in Theorem A' which appears later and is due to Sahney (8).

Let X be a compact differentiable n-manifold of class C∞ and let f be a C∞ map of X into euclidean (n + k)-space. Then f is an immersion if its jacobian has rank n at each point of X. It is an embedding if it is also one-one. We write X ⊆ n + k to denote the existence of an immersion, X ⊂ n + k to denote the existence of an embedding. By a theorem of Whitney, we have X ⊆ 2n − 1, X ⊂ 2n.

It was shown by Birkhoff ((1), p. 253) that every spherically symmetric solution of the field equations of general relativity for empty space,

may be reduced, by suitable coordinate transformations, to the static Schwarzschild form:

where m is a constant. This result is known as Birkhoff's theorem and excludes the possibility of spherically symmetric gravitational radiation. Different proofs of the theorem have been given by Eiesland(2), Tolman(3), and Bonnor ((4), p. 167).

An alternative procedure is developed for examining the solutions of the Low equation. The ambiguities of those solutions which have a finite number of zeros are shown to satisfy the conditions derived earlier by Castillejo, Dalitz and Dyson. The method presented here has the advantage that it makes no special use of the positiveness of the cut-off function, and so can be used when this function changes sign. It is shown that the arbitrariness of the solution increases with the number of these sign changes, but that a completely negative cut-off function still satisfies the CDD conditions.

The familiar classical dynamical theory treats only a restricted class of dynamical systems. For a Lagrangian depending on n generalized coordinates, the n generalized velocities, and (perhaps) the time the usual theory considers only the normal case in which the Hessian matrix of the Lagrangian with respect to the generalized velocities has rank n. But the rank of this Hessian matrix can be less than n in a given dynamical system. Dynamical systems with this property are called degenerate in the present work. Some important physical systems do in fact belong to this degenerate class: for instance, Einstein's theory of the gravitational field, the theory of the electromagnetic field in terms of the electromagnetic potentials, and the theory of the neutral vector meson field. This circumstance makes it necessary to have a general theory of degenerate dynamical systems (and of the associated degenerate variational problems).

Given an ‘extraordinary cohomology theory’, that is, a cohomology theory satisfying all the axioms of Eilenberg and Steenrod (7) except the dimension axiom, it is well known that there exists a spectral sequence relating the ordinary cohomology of a space with the extraordinary theory (see, for example, (3) in the case of K*(X)). Obviously, it would be useful to know the differentials in this spectral sequence, and it is the purpose of this paper to identify them in terms of cohomology operations defined by certain k-invariants. We shall make use of E. H. Brown's recent theorem (5) on the representability of extraordinary cohomology theories, to construct a second spectral sequence, in which the differentials are readily identifiable, which we shall prove is isomorphic to the usual one.

The following properties of the real numbers are well known:

If (xn) is a sequence of real numbers, xn → x and xn ≥ 0 for each n then x > 0. (1)

If (xn) is a sequence of real numbers, xn → x and x > 0 then, for all sufficiently large n,xn > 0.

A copositive quadratic form is a real form which is non-negative for non-negative arguments. A completely positive quadratic form is a real form which can be written as a sum of squares of non-negative real forms. The completely positive forms are basic in the study of block designs arising in combinatorial analysis (3). The copositive forms arise in the theory of inequalities and have been considered in a paper by Mordell (4) and two papers by Diananda(1, 2).

The theory of Fourier transforms

can be developed from the functional equation K(s) K(1 – s) = 1, where K(s) is the Mellin transform of the kernel k(x).

In this paper I show that reciprocities can be obtained which are analogous to the Fourier transforms above but which develop from the much more general functional equation

The reciprocities are obtained by using fractional integration. In addition to the reciprocities we have analogues of the Parseval theorem and of the discontinuous integrals usually associated with Fourier transforms.

In order to simplify the analysis I confine myself to the case n = 1 and to L2 space.

Let A be a right Λ-complex and C be a left Λ-complex where Λ is a ring which is both left and right hereditary; a principal ideal domain is a special case of such a ring. This paper is concerned with the Künneth theorem expressing the homology H(A⊗C) of the product complex A⊗C (= A⊗ΛC) in terms of H(A) and H(C). Any notations we do not explain are those of (1).

The 4-dimensional tensor calculus is used to derive the retarded fields of an accelerated electric dipole of constant moment. Following the analogous case of the accelerated charge, it is shown that the result can be expressed concisely in terms of ordinary three-vectors. The radiation field is discussed for important cases including that of the slowly moving dipole. Cases are cited to exhibit the existence of a forward beam of radiation for uniform circular motion.

Throughout this paper q1,q2,… are positive and x1,x2,… non-negative real numbers. When q1+…+ qn = 1, we define Δn, Sn and Σn as follows:

and

We use the term ‘comparable’ in Kober's(2) sense. Two functions f(x1, …, xn) and g(x1, …, xn) are comparable if and only if αg ≤ f ≤ βg for some positive constants α and β.

Asymptotic expansions of certain generalized Bernoulli polynomials are obtained, some in terms of elementary functions and others in terms of gamma functions and their derivatives. The latter results can also be written in terms of elementary functions, by using the known asymptotic expansions of the gamma functions, and the leading terms are obtained in this way. The results obtained give the asymptotic form of the coefficients occurring in all the usual central-difference formulae of the calculus of finite differences.

It was pointed out by Copson(1) in 1947 that the solution of the integral equation for the electrostatic problem for a circular disc could be reduced to the solution of Abel integral equations and hence a solution obtained in a fairly elementary manner. This result was obtained independently by Lebedev(2), who also obtained a similar result for the electrostatic problem for the spherical cap. The solution for the spherical cap was also obtained independently by Collins (3). In view of the relative simplicity of the approach it seems to be of interest to examine whether there exist other integral equations which can be treated in a similar fashion. In the present paper one such class of integral equations will be considered.

A derivation is given of the general solution of the static baryon Low equation for KΛ-scattering. This model has previously been used by Low to indicate possible ambiguities in the terms elementary and bound-state as applied to particles. The solution derived here can be used to establish this result from a general viewpoint which may possibly be applicable to more realistic models.