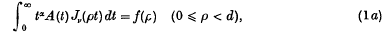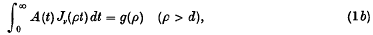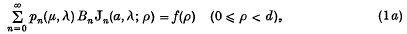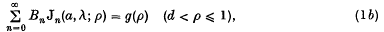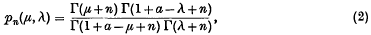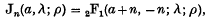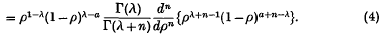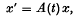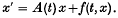Research Article
Basic series corresponding to a class of hypergeometric polynomials†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 599-605
-
- Article
- Export citation
Some formulae for the G -function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-350
-
- Article
- Export citation
Statistical mechanics of a one-dimensional Coulomb system with a uniform charge background
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 779-787
-
- Article
- Export citation
Approximate integration of rapidly oscillating functions and of periodic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-88
-
- Article
- Export citation
The propagator for a particle in the presence of a one-dimensional square-well potential
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 607-613
-
- Article
- Export citation
The solution of Bessel function dual integral equations by a multiplying-factor method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-362
-
- Article
- Export citation
The effect of heat transfer on boundary-layer growth
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 789-802
-
- Article
- Export citation
On Coulomb wave functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-94
-
- Article
- Export citation
The motion of a non-conducting sphere through a conducting fluid in a magnetic cross-field*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 615-624
-
- Article
- Export citation
Some dual series equations involving Jacobi polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-371
-
- Article
- Export citation
On axially symmetric waves: III. Elastic waves in a half-space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 803-809
-
- Article
- Export citation
Uniform approximate solutions of certain nth-order differential equations. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-110
-
- Article
- Export citation
Two-dimensional elliptic inclusions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 811-820
-
- Article
- Export citation
On the motion of a sphere through a conducting fluid in the presence of a magnetic field*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 625-635
-
- Article
- Export citation
Further results for the solutions of a third-order differential equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-116
-
- Article
- Export citation
Differential equations in Banach spaces and the extension of Lyapunov's method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-381
-
- Article
- Export citation
On axially symmetric waves: I. Linearized compressible flow with axial boundary conditions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 637-654
-
- Article
- Export citation
The vibrations of three two-dimensional lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-396
-
- Article
- Export citation
Elliptic inclusions in a stressed matrix
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 821-832
-
- Article
- Export citation
The solution of an infinite set of differential-difference equations occurring in polymerization and queueing problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-124
-
- Article
- Export citation

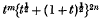 where
where