Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T08:25:49.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Computation with classical sequents

Published online by Cambridge University Press:  01 June 2008

STEFFEN VAN BAKEL  and
PIERRE LESCANNE
STEFFEN VAN BAKEL
Affiliation:
Department of Computing, Imperial College London, 180 Queen's Gate London SW7 2BZ, U.K. Email: svb@doc.ic.ac.uk
PIERRE LESCANNE
Affiliation:
École Normale Supérieure de Lyon, 46 Allée d'Italie 69364 Lyon 07, France Email: Pierre.Lescanne@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

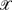is an untyped continuation-style formal language with a typed subset that provides a Curry–Howard isomorphism for a sequent calculus for implicative classical logic. 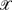can also be viewed as a language for describing nets by composition of basic components connected by wires. These features make 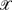an expressive platform on which many different (applicative) programming paradigms can be mapped. In this paper we will present the syntax and reduction rules for 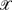; in order to demonstrate its expressive power, we will show how elaborate calculi can be embedded, such as the λ-calculus, Bloo and Rose's calculus of explicit substitutions λx, Parigot's λμ and Curien and Herbelin's .

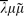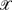was first presented in Lengrand (2003), where it was called the λξ-calculus. It can be seen as the pure untyped computational content of the reduction system for the implicative classical sequent calculus of Urban (2000).

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 18 , Special Issue 3: Rewriting calculi, higher-order reductions and patterns , June 2008 , pp. 555 - 609
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadi, M., Cardelli, L., Curien, P.-L. and Lévy, J.-J. (1991) Explicit substitutions. Journal of Functional Programming 1 (4)375–416.CrossRefGoogle Scholar
Aho, A. V., Sethi, R. and Ullman, J. D. (1988) Compilers: Principles, Techniques and Tools, Addison-Wesley.Google Scholar
Appel, A. W. and Jim, T. (1989) Continuation-passing, closure-passing style. In: Proceedings of the 16th ACM SIGPLAN-SIGACT symposium on Principles of Programming languages, ACM Press 293–302.CrossRefGoogle Scholar
Ariola, Z. M. and Herbelin, H. (2003) Minimal classical logic and control operators. In: Baeten, J. C. M., Lenstra, J. K., Parrow, J. and Woeginger, G. J. (eds.) ICALP. Springer-Verlag Lecture Notes in Computer Science 2719 871–885.Google Scholar
Ariola, Z. M., Herbelin, H. and Sabry, A. (2004) A type-theoretic foundation of continuations and prompts. In: Proceedings of the Ninth ACM SIGPLAN International Conference on Functional Programming (ICFP'04), ACM 40–53.Google Scholar
Audebaud, P. and van Bakel, S. (2006) Understanding with λμ. Consistent interpretations of the implicative sequent calculus in natural deduction (submitted).Google Scholar
van Bakel, S., Lengrand, S. and Lescanne, P. (2005) The language : circuits, computations and classical logic. In: Coppo, M., Lodi, E. and Pinna, G. M. (eds.) Proceedings of Ninth Italian Conference on Theoretical Computer Science (ICTCS'05), Siena, Italy. Springer-Verlag Lecture Notes in Computer Science 370181–96.Google Scholar
van Bakel, S. and Raghunandan, J. (2005) Implementing . Electronic Proceedings of Second International Workshop on Term Graph Rewriting 2004 (TermGraph'04). Electronic Notes in Theoretical Computer Science.Google Scholar
van Bakel, S. and Raghunandan, J. (2006) Capture avoidance and garbage collection for . Presented at the Third International Workshop on Term Graph Rewriting 2006 (TermGraph'06), Vienna, Austria.Google Scholar
Barbanera, F. and Berardi, S. (1996) A symmetric lambda calculus for classical program extraction. Information and Computation 125 (2)103–117.CrossRefGoogle Scholar
Barendregt, H. (1984) The Lambda Calculus: its Syntax and Semantics, revised edition, North-Holland.Google Scholar
Barendregt, H. and Ghilezan, S. (2000) Lambda terms for natural deduction, sequent calculus and cut-elimination. Journal of Functional Porgramming 10 (1)121–134.Google Scholar
Bloo, R. and Geuvers, J. H. (1996) Explicit substitution: on the edge of strong normalisation. Computing Science Reports 96–10, Eindhoven University of Technology, The Netherlands. (To appear in Theoretical Computer Science.)Google Scholar
Bloo, R. and Rose, K. (1995) Preservation of strong normalisation in named lambda calculi with explicit substitution and garbage collection. CSN'95 – Computer Science in the Netherlands 62–72. (Available at ftp://ftp.diku.dk/diku/semantics/papers/D-246.ps.)Google Scholar
de Bruijn, N. G. (1978) A namefree lambda calculus with facilities for internal definition of expressions and segments. TH-Report 78-WSK-03, Technological University Eindhoven, Netherlands, Department of Mathematics.Google Scholar
Church, A. (1940) A formulation of the simple theory of types. The journal of Symbolic Logic 5 56–68.CrossRefGoogle Scholar
Clement, D. (1986) A Simple Applicative Language: MINI-ML. Technical Report 529, INRIA centre Sophia Antipolis (France).Google Scholar
Coquand, T. and Huet, G. P. (1985) Constructions: A higher order proof system for mechanizing mathematics. European Conference on Computer Algebra (1) 151–184.Google Scholar
Curien, P.-L. and Herbelin, H. (2000) The Duality of Computation. In: Proc. of the 5th ACM SIGPLAN International Conference on Functional Programming (ICFP'00), ACM 233–243. (A corrected version is available from http://yquem.inria.fr/herbelin/publis/icfp-CuHer00-duality+errata.ps.gz)Google Scholar
Curry, H. B., Feys, R. and Craig, W. (1958) Combinatory Logic, Vol. 1, Elsevier Science Publishers B.V.Google Scholar
van Dalen, D. (1994) Logic and Structure, Springer-Verlag.CrossRefGoogle Scholar
Danos, V., Joinet, J.-B. and Schellinx, H. (1996) Computational isomorphisms in classical logic (extended abstract). Electronic Notes in Theoretical Computer Science 3.Google Scholar
Danos, V., Joinet, J.-B. and Schellinx, H. (1997) A new deconstructive logic: Linear logic. The journal of Symbolic Logic 62.Google Scholar
Gentzen, G. (1935) Untersuchungen über das Logische Schliessen. Mathematische Zeitschrift 39 176–210 and 405–431. (English translation in Szabo (1969, Pages 68–131)).CrossRefGoogle Scholar
Ghilezan, S. and Lescanne, P. (2004) Classical proofs, typed processes and intersection types. In: Berardi, S., Coppo, M. and Damiani, F. (eds.) TYPES'03 (to appear in Springer-Verlag Lecture Notes in Computer Science).CrossRefGoogle Scholar
Girard, J. Y. (1986) The system F of variable types, fifteen years later. Theoretical Computer Science 45 159–192.Google Scholar
Girard, J.-Y. (1987) Linear logic. Theoretical Computer Science 50 1–102.CrossRefGoogle Scholar
Girard, J.-Y. (1991) A new constrcutive logic: classical logic. Mathematical Structures in Computer Science 1 (3)255–296.Google Scholar
Griffin, T. (1990) A formulae-as-types notion of control. In: Proceedings of the 17th Annual ACM Symposium on Principles Of Programming Languages 47–58.CrossRefGoogle Scholar
de Groote, P. (1994) On the relation between the λμ-calculus and the syntactic theory of sequential control. In: Proceedings of the 5th International Conference on Logic Programming and Automated Reasoning, (LPAR'94). Springer-Verlag Lecture Notes in Computer Science 822 31–43.Google Scholar
Herbelin, H. (1995) Séquents qu'on calcule : de l'interprétation du calcul des séquents comme calcul de λ-termes et comme calcul de stratégies gagnantes, Thèse d'université, Université Paris 7.Google Scholar
Herbelin, H. (2005) C'est maintenant qu'on calcule: au cœur de la dualité, Mémoire d'habilitation, Université Paris 11.Google Scholar
Krivine, J.-L. (1994) Classical logic, storage operators and second-order lambda-calculus. Ann. Pure Appl. Logic 68 (1)53–78.CrossRefGoogle Scholar
Lengrand, S. (2002) A computational interpretation of the cut-rule in classical sequent calculus, Master's thesis, Mathematical Institute and Computing Laboratory, University of Oxford.Google Scholar
Lengrand, S. (2003) Call-by-value, call-by-name, and strong normalization for the classical sequent calculus. In: Gramlich, B. and Lucas, S. (eds.) Post-proceedings of the 3rd Workshop on Reduction Strategies in Rewriting and Programming (WRS 2003). Electronic Notes in Theoretical Computer Science 86.Google Scholar
Lengrand, S. (2006) Normalisation & Equivalence in Proof Theory & Type Theory, Ph.D. thesis, University of Paris VII and University of St Andrews.Google Scholar
Lengrand, S., Lescanne, P., Dougherty, D., Dezani-Ciancaglini, M. and van Bakel, S. (2004) Intersection types for explicit substitutions. Information and Computation 189 (1)17–42.Google Scholar
Lescanne, P. (1994) From λσ to λυ, a journey through calculi of explicit substitutions. In: Boehm, H. (ed.) Proceedings of the 21st Annual ACM Symposium on Principles Of Programming Languages, ACM 60–69.Google Scholar
Ong, C.-H. L. and Stewart, C. A. (1997) A Curry-Howard foundation for functional computation with control. In: Proceedings of the 24th Annual ACM Symposium on Principles Of Programming Languages 215–227.CrossRefGoogle Scholar
Parigot, M. (1992) An algorithmic interpretation of classical natural deduction. In: Proc. of Int. Conf. on Logic Programming and Automated Reasoning, LPAR'92. Springer-Verlag Lecture Notes in Computer Science 624 190–201.CrossRefGoogle Scholar
Parigot, M. (1993) Classical proofs as programs. Kurt Gödel Colloquium 263–276. (Presented at TYPES Workshop, at Bǎstad, June 1992.)CrossRefGoogle Scholar
Raghunandan, J. and Summers, A. (2006) On the Computational Representation of Classical Logical Connectives. (Presented at 2nd International Workshop on Developments in Computational Models (DCM 2006), Venice, Italy.)Google Scholar
Summers, A. and vanBakel, S. (2006) Approaches to polymorphism in classical sequent calculus. In: Sestoft, P. (ed.) Proceedings of 15th European Symposium on Programming (ESOP'06). Springer-Verlag Lecture Notes in Computer Science 3924 84–99.Google Scholar
Szabo, M. E. (ed.) (1969) The Collected Papers of Gerhard Gentzen, Studies in Logic and the Foundations of Mathematics, North-Holland.Google Scholar
Urban, C. (2000) Classical Logic and Computation, Ph.D. thesis, University of Cambridge.Google Scholar
Urban, C. (2001) Strong Normalisation for a Gentzen-like Cut-Elimination Procedure. In: Proceedings of Typed Lambda Calculus and Applications (TLCA'01). Springer-Verlag Lecture Notes in Computer Science 2044 415–429.CrossRefGoogle Scholar
Urban, C. and Bierman, G. M. (2001) Strong normalisation of cut-elimination in classical logic. Fundamentae Informaticae 45 (1,2)123–155.Google Scholar
Wadler, P. (2003) Call-by-Value is Dual to Call-by-Name. In: Proceedings of the eighth ACM SIGPLAN international conference on Functional programming 189 – 201.Google Scholar
Whitehead, A. N. and Russell, B. (1925) Principia Mathematica, 2nd edition, Cambridge University Press.Google Scholar
Whitehead, A. N. and Russell, B. (1997) Principia Mathematica to *56, 2nd edition, Cambridge Mathematical Library, Cambridge University Press.CrossRefGoogle Scholar