Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-11T07:11:25.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability in the local structure of the ω-Turing degrees

Published online by Cambridge University Press:  21 February 2019

Hristo Ganchev  and
Andrey C. Sariev
Hristo Ganchev
Affiliation:
Faculty of Mathematics and Informatics, Sofia University, Sofia, Bulgaria
Andrey C. Sariev*
Affiliation:
Faculty of Mathematics and Informatics, Sofia University, Sofia, Bulgaria
*
*Corresponding author. Email: andreys@fmi.uni-sofia.bg
Get access Rights & Permissions [Opens in a new window]

Abstract

This article continues the study of the definability in the local substructure 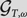$\mathcal{G}_{T,\omega}$ of the ω-Turing degrees, initiated in (Sariev and Ganchev 2014). We show that the class I of the intermediate degrees is definable in 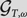$\mathcal{G}_{T,\omega}$.

Keywords

Turing reducibilityω-Turing degreesdegree structuresdefinabilityjump classes
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 29 , Issue 7 , August 2019 , pp. 927 - 937
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cooper, S. B. (1972). Distinguishing the Arithmetical Hierarchy. preprint.Google Scholar
Ganchev, H. and Sariev, A. C. (2015). Definability of jump classes in the local theory of the ω-enumeration degrees. Annuaire de Université de Sofia, Faculté de Mathématiques et Informatique 102 115–132.Google Scholar
Ganchev, H. and Soskova, M. I. (2012). The high/low hierarchy in the local structure of the ω-enumeration degrees. Annals of Pure and Applied Logic 163 (5) 547–566.CrossRefGoogle Scholar
Posner, D. B. and Robinson, R.W. (1981). Degrees joining to 0ʹ. Journal of Symbolic Logic 46 (4) 714–722.CrossRefGoogle Scholar
Sariev, A. C. and Ganchev, H. (2014). The ω-Turing degrees. Annals of Pure and Applied Logic 165 (9) 1512–1532.CrossRefGoogle Scholar
Soare, R. S. (1974). Automorphisms of the lattice of recursively enumerable sets. Bulletin of the American Mathematical Society 80 53–58.CrossRefGoogle Scholar
Soskov, I. N. (2007). The ω-enumeration degrees. Journal of Logic and Computation 17 (6) 1193–1214.CrossRefGoogle Scholar