Inclusions for partiality

Abstract

In this paper we introduce stable systems of inclusions, which feature chosen arrows A ↪ B to capture the notion that A is a subobject of B, and proposes them as an alternative context to stable systems of monics to discuss partiality. A category C equipped with such a system 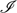$\mathscr{I}$, called an i-category, is shown to give rise to an associated category ∂(C,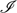$\mathscr{I}$) of partial maps, which is a split restriction category whose restriction monics are inclusions. This association is the object part of a 2-equivalence between such inclusively split restriction categories and i-categories. 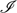$\mathscr{I}$ determines a stable system of monics 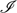$\mathscr{I}$⁺ on C, and, conversely, a stable system of monics 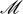$\mathscr{M}$ on C yields an i-category (C[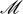$\mathscr{M}$],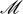$\mathscr{M}$⁺), giving a 2-adjunction between i-categories and m-categories. The category of partial maps Par(C,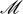$\mathscr{M}$) is isomorphic to the full subcategory of ∂(C[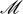$\mathscr{M}$],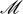$\mathscr{M}$⁺) comprising the objects of C, and ∂(C,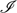$\mathscr{I}$) ≅ Par(C,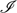$\mathscr{I}$⁺).