Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T09:33:46.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Kan injectivity in order-enriched categories

Published online by Cambridge University Press:  02 December 2014

JIŘÍ ADÁMEK ,
LURDES SOUSA  and
JIŘÍ VELEBIL
JIŘÍ ADÁMEK
Affiliation:
Institute of Theoretical Computer Science, Technical University of Braunschweig, Braunschweig, Germany Email: adamek@iti.cs.tu-bs.de
LURDES SOUSA
Affiliation:
Polytechnic Institute of Viseu and Centre for Mathematics of the University of Coimbra, Coimbra, Portugal Email: sousa@estv.ipv.pt
JIŘÍ VELEBIL
Affiliation:
Department of Mathematics, Faculty of Electrical Engineering, Czech Technical University in Prague, Prague, Czech Republic Email: velebil@math.feld.cvut.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

Continuous lattices were characterised by Martín Escardó as precisely those objects that are Kan-injective with respect to a certain class of morphisms. In this paper we study Kan-injectivity in general categories enriched in posets. As an example, ω-CPO's are precisely the posets that are Kan-injective with respect to the embeddings ω ↪ ω + 1 and 0 ↪ 1.

For every class 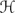$\mathcal{H}$ of morphisms, we study the subcategory of all objects that are Kan-injective with respect to 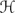$\mathcal{H}$ and all morphisms preserving Kan extensions. For categories such as Top0 and Pos, we prove that whenever 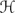$\mathcal{H}$ is a set of morphisms, the above subcategory is monadic, and the monad it creates is a Kock–Zöberlein monad. However, this does not generalise to proper classes, and we present a class of continuous mappings in Top0 for which Kan-injectivity does not yield a monadic category.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 25 , Issue 1 , January 2015 , pp. 6 - 45
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adámek, J. and Rosický, J. (1988) Intersections of reflective subcategories. Proceedings of the American Mathematical Society 103 710–712.CrossRefGoogle Scholar
Adámek, J. and Rosický, J. (1994) Locally presentable and accessible categories, Cambridge University Press.CrossRefGoogle Scholar
Adámek, J., Hébert, M. and Sousa, L. (2009) The orthogonal subcategory problem and the small object argument. Applied Categorical Structures 17 211–246.Google Scholar
Adámek, J., Herrlich, H. and Strecker, G. E. (1990) Abstract and concrete categories, John Wiley and Sons. (Also, Reprints in Theory and Applications of Categories (2006) 171–507.)Google Scholar
Adámek, J., Herrlich, H., Rosický, J. and Tholen, W. (2002) On a generalized small-object argument for the injective subcategory problem. Cahiers de Topologie et Geométrie Différentielle Catégoriques XLIII 83–106.Google Scholar
Banaschewski, B. (1977) Essential extensions of T 0-spaces. General Topology and Applications 7 (3)233–246.CrossRefGoogle Scholar
Banaschewski, B. and Bruns, G. (1967) Categorical characterisation of the MacNeille completion. Archiv der Mathematik 18 369–377.Google Scholar
Bunge, M. and Funk, J. (1999) On a bicomma object condition for KZ-doctrines. Journal of Pure and Applied Algebra 143 69–105.Google Scholar
Carvalho, M. and Sousa, L. (2011) Order-preserving reflectors and injectivity. Topology and its Applications 158 (17)2408–2422.CrossRefGoogle Scholar
Day, A. (1975) Filter monads, continuous lattices and closure systems. Canadian Journal of Mathematics 27 50–59.CrossRefGoogle Scholar
Erker, T. (1998) Right Kan spaces and essentially complete T 0-spaces. Electronic Notes in Theoretical Computer Science 13 41–52.CrossRefGoogle Scholar
Escardó, M. H. (1997) Injective spaces via the filter monad. In: Proceedings of the 12th Summer Conference on General Topology and its Applications.Google Scholar
Escardó, M. H. (1998) Properly injective spaces and function spaces. Topology and its Applications 89 (1–2)75–120.CrossRefGoogle Scholar
Escardó, M. H. (2003) Injective locales over perfect embeddings and algebras of the upper powerlocale monad. Applied General Topology 4 (1)193–200.Google Scholar
Escardó, M. H. and Flagg, R. C. (1999) Semantic domains, injective spaces and monads. Electronic Notes in Theoretical Computer Science 20.Google Scholar
Freyd, P. J. and Kelly, G. M. (1972) Categories of continuous functors I. Journal of Pure and Applied Algebra 2 169–191.CrossRefGoogle Scholar
Hoffmann, R.-E. (1979) Essentially complete T 0-spaces. Manuscripta Mathematica 27 (4)401–432.CrossRefGoogle Scholar
Kelly, G. M. (1980) A unified treatment of transfinite constructions for free algebras, free monoids, colimits, associated sheaves, and so on. Bulletin of the Australian Mathematical Society 22 1–83.CrossRefGoogle Scholar
Kelly, G. M. (1982) Basic concepts of enriched category theory, London Mathematical Society Lecture Notes Series 64, Cambridge University Press. (Also, Reprints in Theory and Applications of Categories (2005) 101–136.)Google Scholar
Kock, A. (1995) Monads for which structures are adjoint to units (version 3). Journal of Pure and Applied Algebra 104 41–59.CrossRefGoogle Scholar
Koubek, V. (1975) Every concrete category has a representation by T 2 paracompact spaces. Commentationes Mathematicae Universitatis Carolinae 15 655–664.Google Scholar
Koubek, V. and Reiterman, J. (1979) Categorical constructions of free algebras, colimits, and completions of partial algebras. Journal of Pure and Applied Algebra 14 195–231.Google Scholar
Lack, S. (2009) A 2-categories companion. In: Baez, J. C. and May, J. P. (eds.) Towards higher categories, Springer.Google Scholar
Mac Lane, S. (1998) Categories for the working mathematician, 2nd edition, Springer.Google Scholar
Reiterman, J. (1976) Categorical algebraic constructions, Ph.D. Thesis (in Czech), Charles University, Prague.Google Scholar
Scott, D. S. (1972) Continuous lattices. In: Lawvere, F. W. (ed.) Toposes, algebraic geometry and logic. Springer-Verlag Lecture Notes in Mathematics 274 97–136.Google Scholar
Smyth, M. B. and Plotkin, G. D. (1982) The category-theoretic solution of recursive domain equations. SIAM Journal on Computing 11 761–783.CrossRefGoogle Scholar
Wyler, O. (1984) Compact ordered spaces and prime Wallman compactifications. In: Categorical Topology, Heldermann 618–635.Google Scholar
Zöberlein, V. (1976) Doctrines on 2-categories. Mathematische Zeitschrift 148 267–279.CrossRefGoogle Scholar