Article contents
Least fixpoints of endofunctors of cartesian closed categories
Published online by Cambridge University Press: 04 March 2009
Abstract
Least fixpoints are constructed for finite coproducts of definable endofunctors of Cartesian closed categories that have weak polynomial products and joint equalizers of arbitrary families of pairs of parallel arrows. Both conditions hold in PER, the category whose objects are partial equivalence relations on N, and whose arrows are partial recursive functions. Weak polynomial products exist in any cartesian closed category with a finite number of objects as well as in any model of second order polymorphic lambda calculus: that is, in the proof theory of any second order positive intuitionistic propositional calculus, but such a category need not have equalizers. However, any finite coproduct of definable endofunctors of a cartesian closed category 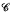 with weak polynomial products will have a least fixpoint in a larger category
with weak polynomial products will have a least fixpoint in a larger category 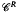 with equalizers whose objects are right ideals (or sieves) of
with equalizers whose objects are right ideals (or sieves) of 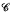 modulo certain congruence relations, and whose arrows are induced from
modulo certain congruence relations, and whose arrows are induced from 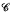 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1993
References
- 5
- Cited by

