Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T09:11:47.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordered combinatory algebras and realizability†

Published online by Cambridge University Press:  10 September 2015

WALTER FERRER SANTOS ,
JONAS FREY ,
MAURICIO GUILLERMO ,
OCTAVIO MALHERBE  and
ALEXANDRE MIQUEL
WALTER FERRER SANTOS
Affiliation:
Centro de Matemática. Facultad de Ciencias. Universidad de la República, Montevideo, Uruguay
JONAS FREY
Affiliation:
Department of Computer Science. University of Copenhagen. Universitetsparken 1. København Ø
MAURICIO GUILLERMO
Affiliation:
Instituto de Matemática y Estadística Rafael Laguardia. Facultad de Ingeniería. Universidad de la República, Montevideo, Uruguay
OCTAVIO MALHERBE
Affiliation:
Instituto de Matemática y Estadística Rafael Laguardia. Facultad de Ingeniería. Universidad de la República, Montevideo, Uruguay
ALEXANDRE MIQUEL
Affiliation:
Instituto de Matemática y Estadística Rafael Laguardia. Facultad de Ingeniería. Universidad de la República, Montevideo, Uruguay
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose the new concept of Krivine ordered combinatory algebra (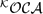$\mathcal{^KOCA}$) as foundation for the categorical study of Krivine's classical realizability, as initiated by Streicher (2013).

We show that 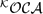$\mathcal{^KOCA}$'s are equivalent to Streicher's abstract Krivine structures for the purpose of modeling higher-order logic, in the precise sense that they give rise to the same class of triposes. The difference between the two representations is that the elements of a 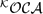$\mathcal{^KOCA}$ play both the role of truth values and realizers, whereas truth values are sets of realizers in 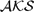$\mathcal{AKS}$s.

To conclude, we give a direct presentation of the realizability interpretation of a higher order language in a 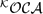$\mathcal{^KOCA}$, which showcases the dual role that is played by the elements of the 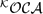$\mathcal{^KOCA}$.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Issue 3 , March 2017 , pp. 428 - 458
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡ This author would like to thank M. Guillermo and the uruguayan government agency ANII, for making possible his visit to Uruguay that resulted in a productive collaboration.
†

This work was partially supported by ANII (Ur), CSIC (Ur), IFUM (Fr/Ur), ANR (Fr).

References

Bell, J.L. (1977) Boolean-valued models and independence proofs in set theory Oxford Logic Guides n. 4, Clarendon Press, Oxford.Google Scholar
Birkhoff, G. (1955) Lattice theory Colloquium Publications, Vol 25, American Mathematical Society, Third edition.Google Scholar
Friedman, H. (1973) Some applications of Kleene's methods for intuitionistic system, Cambridge summer school in mathematics, 337, pp 113–170.Google Scholar
Gierz, G., Hofmann, K. H., Keimel, K., Lawson, J.D., Mislove, M. and Scott, D. S. (2003) Continuous Lattices and Domains. Cambridge University Press, 2003.Google Scholar
Griffin, T.G. (1990) A Formulæ-as-Types Notion of Control. In Conference Record of the Seventeenth Annual ACM Symposium on Principles of Programming Languages.Google Scholar
Hofstra, P. (2006) All realizability is relative, Math. Proc. Cambridge Philos. Soc. 141, no. 2, pp. 239–264.CrossRefGoogle Scholar
Hofstra, P. (2008) Iterated realizability as a comma construction, Math. Proc. Cambridge Philos. Soc. 144, no. 1, pp. 39–51.Google Scholar
Hyland, J.M.E. (1982) The effective topos, Proc. of The L.E.J. Brouwer Centenary Symposium (Noordwijkerhout 1981) pp. 165–216, North Holland.Google Scholar
Hyland, J.M.E., Johnstone, P.T. and Pitts, A.M. (1980) Tripos theory, Math. Proc. Cambridge Phil. Soc. 88, pp 205–232.Google Scholar
Johnstone, P.T. (2002) Sketches of an elephant: a topos theory compendium. Vol. 1, volume 43 of Oxford Logic Guides. The Clarendon Press Oxford University Press, New York.Google Scholar
Hofstra, P. and van Oosten, J. (2004) Ordered partial combinatory algebras, Math. Proc. Cambridge Philos. Soc. 134, no. 3, pp. 445–463.Google Scholar
Kleene, S.C. (1945) On the interpretation of intuitionistic number theory., Journal of Symbolic Logic, 10:109–124.CrossRefGoogle Scholar
Krivine, J.L. (1994), A general storage theorem for integers in call-by-name lambda-calculus., Th. Comp. Sc., 129, p. 79–94.Google Scholar
Krivine, J.L. (2001), Realizability algebras: a program to well order $\mathbb R$ , Logical methods in computer science, vol 7, (3: 02), pp 1–47.Google Scholar
Krivine, J.L. (2001) Types lambda-calculus in classical Zermelo-Fraenkel set theory, Arch. Math. Log. 40, no. 3, pp. 189–205.Google Scholar
Krivine, J.L. (2003), Dependent choice, ‘quote’ and the clock, Th. Comp. Sc. 308, pp. 259–276.Google Scholar
Krivine, J.L. (2008) Structures de réalisabilité, RAM et ultrafiltre sur $\mathbb N$ . http://www.pps.jussieu.fr/~krivine/Ultrafiltre.pdf.Google Scholar
Krivine, J.L. (2009) Realizability in classical logic in Interactive models of computation and program behaviour, Panoramas et synthèses 27 (2009), SMF.Google Scholar
Lack, S. (2010) A 2-categories companion. In Towards higher categories, pages 105–191. Springer.Google Scholar
Lawvere, F.W. (1969) Adjointness in foundations. Dialectica, 23 (3–4):281–296.Google Scholar
Lawvere, F. W. (1970) Equality in hyperdoctrines and the comprehension schema as an adjoint functor. Applications of Categorical Algebra, 17:1–14, 1970.Google Scholar
McCarty, D. (1983) Realizability and recursive mathematics, Technical Report CMU-CS-84-131. Departament of Computer Science, Carnegie-Mellon University, 1984. Report version of the author's PhD thesis, Oxford University.Google Scholar
Myhill, J. (1973) Some properties of intuitionistic Zermelo-Fraenkel set theory, Lecture notes in mathematics 337, pp 206–231.Google Scholar
Sørensen, M.H. and Urzyczyn, P. Lectures in the Curry–Howard isomorphism Elsvier, Studies in Logic and the foundations of mathematics, vol 149, 2006.Google Scholar
Streicher, T. (2013) Krivine's Classical Realizability from a Categorical Perspective, Math. Struct. in Comp. Science. vol. 23, n 6.CrossRefGoogle Scholar
Troelstra, A.S. (1973) Metamathematical investigation of intuitionistic arithmetic and analysis, volume 344. Springer Science & Business Media.Google Scholar
van Oosten, J. (2008) Realizability, an Introduction to its Categorical Side, Elsevier.Google Scholar