Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:39:24.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Semantical proofs of correctness for programs performing non-deterministic tests on real numbers

Published online by Cambridge University Press:  27 October 2010

THOMAS ANBERRÉE
THOMAS ANBERRÉE*
Affiliation:
Division of Computer Science, University of Nottingham in Ningbo, China, 199 Taikang Road East, 315100, Ningbo, China Email: thomas.anberree@nottingham.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a functional language that performs non-deterministic tests on real numbers and define a denotational semantics for that language based on Smyth powerdomains. The semantics is only an approximate one because the denotation of a program for a real number may not be precise enough to tell which real number the program computes. However, for many first-order total functions f : 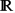n → 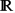, there exists a program for f whose denotation is precise enough to show that the program indeed computes the function f. In practice, it is not difficult to find programs like this that possess a faithful denotation. We provide a few examples of such programs and the corresponding proofs of correctness.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 20 , Special Issue 5: Theory and Applications of Models of Computation (TAMC 2008–2009) , October 2010 , pp. 723 - 751
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramsky, S. and Jung, A. (1994) Domain theory. In: Abramsky, S., Gabbay, D. M. and Maibaum, T. S. E. (eds.) Handbook of Logic in Computer Science 3, Clarendon Press 1–168.Google Scholar
Anberree, T. (2007) A denotational semantics for total correctness of sequential exact real programs, Ph.D. thesis, The University of Birmingham, United Kingdom.Google Scholar
Boehm, H. and Cartwright, R. (1990) Exact real arithmetic: formulating real numbers as functions. In: Research topics in functional programming, Addison-Wesley Longman 43–64.Google Scholar
Brattka, V. (1996) Recursive characterization of computable real-valued functions and relations. Theoretical Computer Science 162 4577.CrossRefGoogle Scholar
Gierz, G., Hofmann, K., Keimel, K., Lawson, J., Mislove, M. and Scott, D. (2003) Continuous Lattices and Domains. Encyclopedia of Mathematics and its Applications, Cambridge University Press 93.Google Scholar
Marcial-Romero, J. (2004) Semantics of a sequential language for exact real-number computation, Ph.D. thesis, The University of Birmingham, United Kingdom.CrossRefGoogle Scholar
Marcial-Romero, J. and Escardó, M. (2007) Semantics of a sequential language for exact real-number computation. Theoretical Computer Science 379 (1–2)120–141.CrossRefGoogle Scholar
Plotkin, G. (1977) LCF considered as a programming language. Theoretical Computer Science 5 (3)225–255.CrossRefGoogle Scholar
Streicher, T. (2006) Domain-Theoretic Foundations of Functional Programming, World Scientific.CrossRefGoogle Scholar
Weihrauch, K. (2000) Computable analysis: an introduction, Springer-Verlag.CrossRefGoogle Scholar