Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T23:52:21.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakest preconditions in fibrations

Published online by Cambridge University Press:  28 October 2022

Alejandro Aguirre ,
Shin-ya Katsumata Open the ORCID record for Shin-ya Katsumata [Opens in a new window]  and
Satoshi Kura
Alejandro Aguirre
Affiliation:
Aarhus University, Åbogade 34, 8200 Aarhus N, Denmark
Shin-ya Katsumata*
Affiliation:
National Institute of Informatics, Chiyoda City 100-8361, Japan
Satoshi Kura
Affiliation:
JSPS Research Fellow and National Institute of Informatics, Chiyoda City 100-8361, Japan
*
*Corresponding author. Email: s-katsumata@nii.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Weakest precondition transformers are useful tools in program verification. One of their key properties is composability, that is, the weakest precondition predicate transformer (wppt for short) associated to program 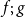$f;\;g$ should be equal to the composition of the wppts associated to f and g. In this paper, we study the categorical structure behind wppts from a fibrational point of view. We characterize the wppts that satisfy composability as the ones constructed from the Cartesian lifting of a monad. We moreover show that Cartesian liftings of monads along lax slice categories bijectively correspond to Eilenberg–Moore monotone algebras. We then instantiate our techniques by deriving wppts for commonplace effects such as the maybe monad, the nonempty powerset monad, the counter monad, or the distribution monad. We also show how to combine them to derive the wppts appearing in the literature of verification of probabilistic programs.

Keywords

Weakest preconditionstrongest postconditionHoare logicmonadfibration
Type
Special Issue: The Power Festschrift
Information
Mathematical Structures in Computer Science , Volume 32 , Special Issue 4: The Power Festschrift , April 2022 , pp. 472 - 510
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramsky, S., Gay, S. and Nagarajan, R. (1996). Specification structures and propositions-as-types for concurrency. In Logics for Concurrency: Structure versus Automata, Berlin, Heidelberg, Springer Berlin Heidelberg, 5–40.CrossRefGoogle Scholar
Aguirre, A., Barthe, G., Hsu, J., Kaminski, B. L., Katoen, J.-P. and Matheja, C. (2021). A pre-expectation calculus for probabilistic sensitivity. Proceedings of the ACM on Programming Languages 5 (POPL) 1–28.CrossRefGoogle Scholar
Aguirre, A. and Katsumata, S. (2020). Weakest preconditions in fibrations. Electronic Notes in Theoretical Computer Science 352 5–27. The 36th Mathematical Foundations of Programming Semantics Conference, 2020.CrossRefGoogle Scholar
Ahman, D., Hritcu, C., Maillard, K., Martnez, G., Plotkin, G. D., Protzenko, J., Rastogi, A. and Swamy, N. (2017). Dijkstra monads for free. In: Castagna, G. and Gordon, A. D. (eds.) Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, Paris, France, January 18–20, 2017, ACM, 515–529.CrossRefGoogle Scholar
Batz, K., Gallus, A., Kaminski, B. L., Katoen, J.-P. and Winkler, T. (2022). Weighted programming: A programming paradigm for specifying mathematical models. Proceedings of the ACM on Programming Languages 6 (OOPSLA1) 1–30.CrossRefGoogle Scholar
Beck, J. (1969). Distributive laws. In: Eckmann, B. (ed.) Seminar on Triples and Categorical Homology Theory, Berlin, Heidelberg, Springer Berlin Heidelberg, 119–140.CrossRefGoogle Scholar
Bonchi, F., König, B. and Petrisan, D. (2018). Up-to techniques for behavioural metrics via fibrations. In: Schewe, S. and Zhang, L. (eds.) 29th International Conference on Concurrency Theory, CONCUR 2018, September 4–7, 2018, Beijing, China, LIPIcs, vol. 118, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, 17:1–17:17.Google Scholar
Dijkstra, E. W. (1975). Guarded commands, nondeterminacy and formal derivation of programs. Communications of the ACM 18 (8) 453–457.CrossRefGoogle Scholar
Filinski, A. (1996). Controlling Effects. Phd thesis, Carnegie Mellon University.Google Scholar
Filinski, A. (2007). On the relations between monadic semantics. Theoretical Computer Science 375 (1–3) 41–75.CrossRefGoogle Scholar
Goncharov, S. and Schröder, L. (2013). A relatively complete generic hoare logic for order-enriched effects. In: 28th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2013, New Orleans, LA, USA, June 25–28, 2013, IEEE Computer Society, 273–282.CrossRefGoogle Scholar
Goubault-Larrecq, J., Lasota, S. and Nowak, D. (2008). Logical relations for monadic types. Mathematical Structures in Computer Science 18 (6) 1169–1217.CrossRefGoogle Scholar
Goy, A. and Petrisan, D. (2020). Combining probabilistic and non-deterministic choice via weak distributive laws. In: Hermanns, H., Zhang, L., Kobayashi, N. and Miller, D. (eds.) LICS’20: 35th Annual ACM/IEEE Symposium on Logic in Computer Science, Saarbrücken, Germany, July 8–11, 2020, ACM, 454–464.Google Scholar
Hasuo, I. (2015). Generic weakest precondition semantics from monads enriched with order. Theoretical Computer Science 604 2–29. Coalgebraic Methods in Computer Science.CrossRefGoogle Scholar
Hermida, C. (1993). Fibrations, Logical Predicates and Indeterminants. Phd thesis, University of Edinburgh.Google Scholar
Hino, W., Kobayashi, H., Hasuo, I. and Jacobs, B. (2016). Healthiness from duality. In: Grohe, M., Koskinen, E. and Shankar, N. (eds.) Proceedings of the 31st Annual ACM/IEEE Symposium on Logic in Computer Science, LICS’16, New York, NY, USA, July 5–8, 2016, ACM, 682–691.CrossRefGoogle Scholar
Jacobs, B. (1994). Semantics of weakening and contraction. Annals of Pure and Applied Logic 69 (1) 73–106.CrossRefGoogle Scholar
Jacobs, B. (1999). Categorical Logic and Type Theory , Studies in Logic and the Foundations of Mathematics, vol. 141, Amsterdam, North Holland.Google Scholar
Joyal, A., Street, R. and Verity, D. (1996). Traced monoidal categories. Mathematical Proceedings of the Cambridge Philosophical Society 119 (3) 447–468.CrossRefGoogle Scholar
Kaminski, B. L., Katoen, J.-P., Matheja, C. and Olmedo, F. (2016). Weakest precondition reasoning for expected run-times of probabilistic programs. In: Thiemann, P. (ed.) Programming Languages and Systems - 25th European Symposium on Programming, ESOP 2016, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2016, Eindhoven, The Netherlands, April 2–8, 2016, Proceedings, Lecture Notes in Computer Science, vol. 9632, Springer, 364–389.CrossRefGoogle Scholar
Katsumata, S. (2005). A semantic formulation of $\top\top$ -lifting and logical predicates for computational metalanguage. In: Proceedings of CSL’05, LNCS, vol. 3634, Springer, 87–102.Google Scholar
Katsumata, S., Sato, T. and Uustalu, T. (2018). Codensity lifting of monads and its dual. Logical Methods in Computer Science 14 (4).Google Scholar
Kock, A. (1970). Strong functors and monoidal monads. Archiv der Mathematik 23 113–120.CrossRefGoogle Scholar
Kura, S. (2022). Semantic Refinements for Program Verification. Phd thesis, The Graduate University for Advanced Studies, SOKENDAI.Google Scholar
Kura, S., Urabe, N. and Hasuo, I. (2019). Tail probabilities for randomized program runtimes via martingales for higher moments. In: Vojnar, T. and Zhang, L. (eds.) Tools and Algorithms for the Construction and Analysis of Systems, Cham, Springer International Publishing, 135–153.Google Scholar
Lane, S. M. and Moerdijk, I. (1994). Sheaves in Geometry and Logic , Universitext, New York, NY, Springer.Google Scholar
Leino, K. R. M. and van de Snepscheut, J. L. A. (1994). Semantics of exceptions. In: Olderog, E.-R. (ed.) Programming Concepts, Methods and Calculi, Proceedings of the IFIP TC2/WG2.1/WG2.2/WG2.3 Working Conference on Programming Concepts, Methods and Calculi (PROCOMET’94) San Miniato, Italy, 6–10 June, 1994, IFIP Transactions, vol. A-56, North-Holland, 447–466.Google Scholar
Leinster, T. (2004). Higher Operads, Higher Categories , London Mathematical Society Lecture Note Series, Cambridge, Cambridge University Press.Google Scholar
MacLane, S. (1998). Categories for the Working Mathematician, 2nd ed., Graduate Texts in Mathematics, vol. 5, New York, NY, Springer.Google Scholar
Maillard, K., Ahman, D., Atkey, R., Martnez, G., Hritcu, C., Rivas, E. and Tanter, É. (2019). Dijkstra monads for all. Proceedings of the ACM on Programming Languages 3 (ICFP) 104:1–104:29.Google Scholar
Maillard, K., Hritcu, C., Rivas, E. and Van Muylder, A. (2020). The next 700 relational program logics. Proceedings of the ACM on Programming Languages 4 (POPL) 4:1–4:33.Google Scholar
Manes, E. and Mulry, P. (2007). Monad compositions I: general constructions and recursive distributive laws. Theory and Applications of Categories 18 172–208.Google Scholar
Martin, U., Mathiesen, E. A. and Oliva, P. (2006). Hoare logic in the abstract. In: Ésik, Z. (ed.) Computer Science Logic, Berlin, Heidelberg, Springer Berlin Heidelberg, 501–515.CrossRefGoogle Scholar
McIver, A. and Morgan, C. (2005). Abstraction, Refinement and Proof for Probabilistic Systems, New York, NY, Springer.Google Scholar
Melliès, P.-A. and Zeilberger, N. (2015). Functors are type refinement systems. In: Rajamani, S. K. and Walker, D. (eds.) Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, Mumbai, India, January 15–17, 2015, ACM, 3–16.CrossRefGoogle Scholar
Moggi, E. (1991). Notions of computation and monads. Information and Computation 93 (1) 55–92.CrossRefGoogle Scholar
Moggi, E. (1995). A semantics for evaluation logic. Fundamenta Informaticae 22 (1/2) 117–152.CrossRefGoogle Scholar
Moggi, E., Taha, W. and Thunberg, J. (2020). Sound over-approximation of probabilities. Acta Cybernetica 24 (3) 269–285.CrossRefGoogle Scholar
Pitts, A. M. (1991). Evaluation Logic. In: van Rijsbergen, C. J. and Birtwistle, G. (eds.) IV Higher Order Workshop, Banff 1990, Workshops in Computing, London, Springer London, 162–189.Google Scholar
Pitts, A. M. (1999). Tripos theory in retrospect. Electronic Notes in Theoretical Computer Science 23 (1) 111–127. Tutorial Workshop on Realizability Semantics and Applications (associated to FLoC’99, the 1999 Federated Logic Conference).Google Scholar
Plotkin, G. and Power, J. (2001). Semantics for algebraic operations. In: Brooks, S. and Mislove, M. (eds.) Proceedings of the Seventeenth Conference on the Mathematical Foundations of Programming Semantics, MFPS 2001, Aarhus, Denmark, May 23–26, 2001, Electronic Notes in Theoretical Computer Science, vol. 45, Elsevier, 332–345.CrossRefGoogle Scholar
Rauch, C., Goncharov, S. and Schröder, L. (2016). Generic hoare logic for order-enriched effects with exceptions. In: James, P. and Roggenbach, M. (eds.) Recent Trends in Algebraic Development Techniques - 23rd IFIP WG 1.3 International Workshop, WADT 2016, Gregynog, UK, September 21–24, 2016, Revised Selected Papers, Lecture Notes in Computer Science, vol. 10644, Springer, 208–222.Google Scholar
Sato, T. (2011). A probabilistic monad with nondeterminism for coalgebraic trace semantics. tetsuya sato. In: CALCO Young Researchers Workshop CALCO-jnr 2011 Selected Papers, University of Southampton.Google Scholar
Sekerinski, E. (2012). Exceptions for dependability. In: Dependability and Computer Engineering: Concepts for Software-Intensive Systems, IGI Global, 11–35.CrossRefGoogle Scholar
Street, R. (1972). The formal theory of monads. Journal of Pure and Applied Algebra 2 (2) 149–168.CrossRefGoogle Scholar
Unno, H., Satake, Y. and Terauchi, T. (2018). Relatively complete refinement type system for verification of higher-order non-deterministic programs. PACMPL 2 (POPL) 12:1–12:29.Google Scholar
Varacca, D. and Winskel, G. (2006). Distributing probability over non-determinism. Mathematical Structures in Computer Science 16 (1) 87–113.CrossRefGoogle Scholar
Voorneveld, N. F. W. (2019). Quantitative logics for equivalence of effectful programs. In: König, B. (ed.) Proceedings of the Thirty-Fifth Conference on the Mathematical Foundations of Programming Semantics, MFPS 2019, London, UK, June 4–7, 2019, Electronic Notes in Theoretical Computer Science, vol. 347, Elsevier, 281–301.CrossRefGoogle Scholar
whiskering Whiskering. https://ncatlab.org/nlab/show/whiskering.Google Scholar
Wolter, U. E., Martini, A. R. and Häusler, E. H. (2020). Indexed and fibred structures for Hoare logic. Electronic Notes in Theoretical Computer Science 348 125–145.CrossRefGoogle Scholar