Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T16:34:34.701Z Has data issue: false hasContentIssue false
  • English
  • Français

Modal descent

Published online by Cambridge University Press:  26 October 2020

Felix Cherubini Open the ORCID record for Felix Cherubini [Opens in a new window]  and
Egbert Rijke
Felix Cherubini*
Affiliation:
Softwareschneiderei GmbH
Egbert Rijke
Affiliation:
University of Ljubljana
*
*Corresponding author. Email: felix.cherubini@posteo.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Any modality in homotopy type theory gives rise to an orthogonal factorization system of which the left class is stable under pullbacks. We show that there is a second orthogonal factorization system associated with any modality, of which the left class is the class of ○-equivalences and the right class is the class of ○-étale maps. This factorization system is called the modal reflective factorization system of a modality, and we give a precise characterization of the orthogonal factorization systems that arise as the modal reflective factorization system of a modality. In the special case of the n-truncation, the modal reflective factorization system has a simple description: we show that the n-étale maps are the maps that are right orthogonal to the map 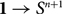$${\rm{1}} \to {\rm{ }}{{\rm{S}}^{n + 1}}$$ . We use the ○-étale maps to prove a modal descent theorem: a map with modal fibers into ○X is the same thing as a ○-étale map into a type X. We conclude with an application to real-cohesive homotopy type theory and remark how ○-étale maps relate to the formally etale maps from algebraic geometry.

Keywords

Homotopy type theorymodal homotopy type theorycohesive homotopy type theoryalgebraic geometryfactorization systems
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Issue 4 , April 2021 , pp. 363 - 391
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anel, M., Biedermann, G., Finster, E. and Joyal, A. (2017). A Generalized Blakers-Massey Theorem. ArXiv e-prints.Google Scholar
Buchholtz, U., van Doorn, F. and Rijke, E. M. (2018). Higher groups in homotopy type theory. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, Association for Computing Machinery, 205–214.10.1145/3209108.3209150CrossRefGoogle Scholar
Cassidy, C., Hébert, M. and Kelly, G. M. (1985). Reflective subcategories, localizations and factorizationa systems. Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics 38 (3) 287–329.10.1017/S1446788700023624CrossRefGoogle Scholar
Christensen, J. D., Opie, M., Rijke, E. M. and Scoccola, L. (2020). Localization in homotopy type theory. Higher Structures 4 (1).Google Scholar
Grothendieck, A. (1960). Éléments de géométrie algébrique.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J. (1967). Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatrième Partie. Publications Mathématiques de l’IHÉS.Google Scholar
Hartshorne, R. (1977). Algebraic Geometry . Graduate Texts in Mathematics. Springer-Verlag.Google Scholar
Hou (Favonia), K.-B. (2017). Higher-Dimensional Types in the Mechanization of Homotopy Theory. PhD thesis.Google Scholar
Khavkine, I. and Schreiber, U. (2017). Synthetic geometry of differential equations: I. Jets and comonad structure. ArXiv e-prints.Google Scholar
Lawvere, F. W. (2007). Axiomatic cohesion. Theory and Applications of Categories 19 41–49.Google Scholar
Myers, D. J. (2019). Good Fibrations through the Modal Prism. arXiv e-prints, arXiv:1908.08034.Google Scholar
Rijke, E. M. (2019). Classifying Types. arXiv e-prints.Google Scholar
Rijke, E. M., Shulman, M. and Spitters, B. (2017). Modalities in Homotopy Type Theory. ArXiv e-prints.Google Scholar
Roberts, D. M. (2009). Fundamental Bigroupoids and 2-Covering Spaces. PhD thesis.Google Scholar
Schreiber, U. (2013). Differential Cohomology in a Cohesive Infinity-Topos.Google Scholar
Schreiber, U. and Shulman, M. (2014). Quantum Gauge Field Theory in Cohesive Homotopy Type Theory. ArXiv e-prints.CrossRefGoogle Scholar
Shulman, M. (2015). Brouwer’s Fixed-Point Theorem in Real-Cohesive Homotopy Type Theory. ArXiv e-prints.Google Scholar
Univalent Foundations, Program (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. Institute for Advanced Study.Google Scholar
Wellen, F. (2017). Formalizing Cartan Geometry in Modal Homotopy Type Theory. PhD thesis, Karlsruhe.Google Scholar