Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stirling, Colin
2013.
Automata, Languages, and Programming.
Vol. 7966,
Issue. ,
p.
398.
Coppo, Mario
Dezani-Ciancaglini, Mariangiola
Díaz-Caro, Alejandro
Margaria, Ines
and
Zacchi, Maddalena
2017.
Retractions in Intersection Types.
Electronic Proceedings in Theoretical Computer Science,
Vol. 242,
Issue. ,
p.
31.

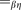 λ
λ