Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T09:17:27.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Probability, valuations, hyperspace: Three monads on top and the support as a morphism

Published online by Cambridge University Press:  08 March 2022

Tobias Fritz ,
Paolo Perrone  and
Sharwin Rezagholi Open the ORCID record for Sharwin Rezagholi [Opens in a new window]
Tobias Fritz
Affiliation:
Department of Mathematics, University of Innsbruck, Innsbruck, Austria
Paolo Perrone
Affiliation:
Department of Computer Science, University of Oxford, Oxford OX1 2JD, UK
Sharwin Rezagholi*
Affiliation:
Faculty of Applied Mathematics and Computer Science, University of Applied Sciences Technikum Wien, Austria Department of Informatics, Higher School of Economics St. Petersburg, Russia
*
*Corresponding author. Email: sharwin.rezagholi@emergentec.com, sharwin.rezagholi@technikum-wien.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider three monads on 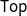$\mathsf{Top}$ , the category of topological spaces, which formalize topological aspects of probability and possibility in categorical terms. The first one is the Hoare hyperspace monad H, which assigns to every space its space of closed subsets equipped with the lower Vietoris topology. The second one is the monad V of continuous valuations, also known as the extended probabilistic powerdomain. We construct both monads in a unified way in terms of double dualization. This reveals a close analogy between them and allows us to prove that the operation of taking the support of a continuous valuation is a morphism of monads 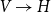$V \to H$ . In particular, this implies that every H-algebra (topological complete semilattice) is also a V-algebra. We show that V can be restricted to a submonad of $\tau$ -smooth probability measures on 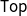$\mathsf{Top}$ . By composing these morphisms of monads, we obtain that taking the supports of $\tau$ -smooth probability measures is also a morphism of monads.

Keywords

Monads on topological spacesvaluationsBorel measuresprobability measureshyperspacesmorphism of monads
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Issue 8 , September 2021 , pp. 850 - 897
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhvlediani, A., Clementino, M. M. and Tholen, W. (2010). On the categorical meaning of Hausdorff and Gromov distances 1. Topology and its Applications 157 (8) 1275–1295. doi: 10.1016/j.topol.2009.06.018.CrossRefGoogle Scholar
Aliprantis, C. D. and Border, K. C. (2006). Infinite Dimensional Analysis, Springer. doi: 10.1007/3-540-29587-9.Google Scholar
Alvarez-Manilla, M., Edalat, A. and Saheb-Djahromi, N. (1998). An extension result for continuous valuations. Electronic Notes in Theoretical Computer Science 13. doi: 10.1016/S1571-0661(05)80210-5.CrossRefGoogle Scholar
Alvarez-Manilla, M., Jung, A. and Keimel, K. (2004). The probabilistic powerdomain for stably compact spaces. Theoretical Computer Science 328 (3) 221–244. doi: 10.1016/j.tcs.2004.06.021.CrossRefGoogle Scholar
Alvarez-Manilla, M. (2002). Extension of valuations on locally compact sober spaces. Topology and its Applications 124 (2) 397–443. doi: 10.1016/S0166-8641(01)00249-8.CrossRefGoogle Scholar
Banakh, T. (1995). The topology of spaces of probability measures 1. Matematychni Studii 5 (1–2) 65–87. Russian.Google Scholar
Beer, G. and Tamaki, R. K. (1993). On hit-and-miss hyperspace topologies. Commentationes Mathematicae Universitatis Carolin 34 (4) 717–728.Google Scholar
Bogachev, V. I. (2000). Measure Theory, Springer. doi: 10.1007/978-3-540-34514-5.Google Scholar
Bledsoe, W. W. and Wilks, C. E. (1972). On Borel product measures. Pacific Journal of Mathematics 42 569–579.CrossRefGoogle Scholar
Cohen, B., Escardo, M. and Keimel, K. (2006). The extended probabilistic powerdomain Monad over stably compact spaces. In: Cai, J.-Y., Barry Cooper, S. and Li, A. (eds.) Theory and Applications of Models of Computation, Springer, 566–575.Google Scholar
Coquand, T. and Spitters, B. (2009). Integrals and valuations. Journal of Logic and Analysis 1 (3) 1–22.Google Scholar
Clementino, M. M. and Tholen, W. (1997). A characterization of the Vietoris topology. Topology Proceedings 22 71–95.Google Scholar
Eilenberg, S. and Moore, J. (1965). Adjoint functors and triples. Illinois Journal of Mathematics 9 381–389.CrossRefGoogle Scholar
EscardÓ, M. and Heckmann, R. (2001). Topologies on spaces of continuous functions. In: Proceedings of the 16th Summer Conference on General Topology and its Applications (New York), vol. 26, 545–564.Google Scholar
EscardÓ, M. (2004). Synthetic topology of data types and classical spaces. Electronic Notes in Theoretical Computer Science 87 21–156. http://www.cs.bham.ac.uk/ mhe/papers/.Google Scholar
Fedorchuk, V. V. (1991). Probability measures in topology. Russian Mathematical Surveys 46 (1) 45–93. doi: 10.1070/rm1991v046n01abeh002722.CrossRefGoogle Scholar
Fremlin, D. H. (2006). Measure Theory. Topological Measure Spaces, vol. 4. Part I, II, Corrected second printing of the 2003 original. Torres Fremlin, Colchester, Part I: 528 pp., Part II: 439+19 pp. (errata).Google Scholar
Fritz, T. and Perrone, P. (2018). Bimonoidal structure of probability Monads. In: Proceedings of MFPS, vol. 34, ENTCS. doi: 10.1016/j.entcs.2018.11.007.CrossRefGoogle Scholar
Fritz, T. and Perrone, P. (2019). A probability monad as the colimit of spaces of finite samples. Theory and Applications of Categories 34 (7) 170–220.Google Scholar
Fritz, T. (2009). Convex Spaces 1: Definition and Examples. arXiv:0903.5522.Google Scholar
Gierz, G. et al. (2003). Continuous Lattices and Domains, Cambridge University Press. doi: 10.1017/CBO9780511542725.Google Scholar
Giry, M. (1982). A categorical approach to probability theory. In: Lecture Notes in Mathematics 915: Categorical Aspects of Topology and Analysis, Springer, 68–85. doi: 10.1007/BFb0092872.Google Scholar
Goubault-Larrecq, J. and Jia, X. (2019). Algebras of the extended probabilistic powerdomain monad. Electronic Notes in Theoretical Computer Science 345 37–61. doi: 10.1016/j.entcs.2019.07.015.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2013). Non-Hausdorff Topology and Domain Theory, Cambridge University Press. doi: 10.1017/CBO9781139524438.Google Scholar
Halmos, P. R. (1950). Measure Theory, Van Nostrand.CrossRefGoogle Scholar
Hausdorff, F. (1914). GrundzÜge der Mengenlehre, Veit und Co., German.Google Scholar
Heckmann, R. (1995). Spaces of valuations. Working paper version. Available at http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.45.5845.Google Scholar
Heckmann, R. (1996). Spaces of valuations. In: Andima, S. et al. (ed.) Papers on General Topology and Applications: Eleventh Summer Conference at the University of Southern Maine, New York Academy of Sciences, 174–200.CrossRefGoogle Scholar
Hofmann, K. H. and Lawson, J. D. (1978). The spectral theory of distributive continuous lattices. Transactions of the American Mathematical Society 246 285–310.CrossRefGoogle Scholar
Hoffmann, R.-E. (1979). Essentially complete T0-spaces. Manuscripta Mathematica 27 (4) 401–432. doi: 10.1007/BF01507294.CrossRefGoogle Scholar
Isbell, J. (1986). General function spaces, products and continuous lattices. Mathematical Proceedings of the Cambridge Philosophical Society 100 (2) 193–205.CrossRefGoogle Scholar
Jacobs, B. (2011). Probabilities, distribution monads, and convex categories. Theoretical Computer Science 412 (28) 3323–3336. doi: 10.1016/j.tcs.2011.04.005.CrossRefGoogle Scholar
Johnstone, P. (1982). Stone Spaces, Cambridge University Press.Google Scholar
Jones, C. and Plotkin, J. D. (1989). A probabilistic powerdomain of evaluations. In: Proceedings of the Fourth Annual Symposium of Logics in Computer Science.Google Scholar
Jung, A. (2004). Stably compact spaces and the probabilistic powerspace construction. In: Desharnais, J. and Panangaden, P. (eds.) Electronic Notes in Theoretical Computer Science 87: Domain-theoretic Methods in Probabilistic Processes, 5–20. doi: 10.1016/j.entcs.2004.10.001.CrossRefGoogle Scholar
Keimel, K. (2008). Topological cones: Functional analysis in a T0-setting. Semigroup Forum 77 109–142. doi:10.1007/s00233-008- 9078-0.CrossRefGoogle Scholar
Keimel, K. (2008). The monad of probability measures over compact ordered spaces and its Eilenberg-Moore algebras. Topology and Applications 156 (2) 227–239. doi: 10.1016/j.topol.2008.07.002.CrossRefGoogle Scholar
Kelly, M. and Lack, S. (1997). On property-like structures. Theory and Applications of Categories 3 (9).Google Scholar
Kirch, O. (1993). Bereiche und Bewertungen. German, MA thesis. Technische Hochschule, Darmstadt.Google Scholar
Kock, A. (2012). Commutative monads as a theory of distributions. Theory and Applications of Categories 26 (4) 97–131.Google Scholar
Kock, A. (1972). Strong functors and monoidal monads. Archiv der Mathematik 23 113–120. doi: 10.1007/BF01304852.CrossRefGoogle Scholar
Kock, A. (1995). Monads for which structures are adjoint to units. Journal of Pure and Applied Algebra 104 41–59. doi: 10.1016/0022-4049(94)00111-U.CrossRefGoogle Scholar
Lawvere, F. W. (1962). The category of probabilistic mappings with applications to stochastic processes, statistics, and pattern recognition. Available at nlab.Google Scholar
Lucyshyn-Wright, R. B. B. (2017). Functional distribution monads in functionalanalytic contexts. Advances in Mathematics 322 806–860. doi: 10.1016/j.aim.2017.09.027.CrossRefGoogle Scholar
Manes, E. (2003). Monads of Sets. In: Hazewinkel, M. (ed.) Handbook of Algebra, vol. 3, Elsevier, 67–153. doi: 10.1016/S1570-7954(03)80059-1.Google Scholar
Michael, E. (1951). Topologies on spaces of subsets. Transactions of the American Mathematical Society 71, 152–182.CrossRefGoogle Scholar
Niefield, S. B. (1982). Cartesianness: Topological spaces, uniform spaces, and affine schemes. Journal of Pure and Applied Algebra 23 146–167. doi: 10.1016/0022-4049(82)90004-4.CrossRefGoogle Scholar
Perrone, P. (2018). Categorical Probability and Stochastic Dominance in Metric Spaces. Available at http://paoloperrone.org/phdthesis.pdf. Phd thesis. University of Leipzig.Google Scholar
Ressel, P. (1977). Some continuity and measurability results on spaces of measures. Mathematica Scandinavica 40 (1) 69–78.CrossRefGoogle Scholar
Rothschild, M. and Stiglitz, J. E. (1970). Increasing risk 1: A definition. Journal of Economic Theory 2 225–243. doi:10.1016/0022-0531(70)90038-4.CrossRefGoogle Scholar
Schalk, A. (1993). Algebras for Generalized Power Constructions. Available at www.cs.man.ac.uk/schalk/publ/diss.ps.gz. Phd thesis. University of Darmstadt.Google Scholar
Smyth, M. B. (1983). Power domains and predicate transformers: A topological view. In: Diaz, J. (ed.) Automata, Languages and Programming. ICALP 1983, Lecture Notes in Computer Science, vol. 154, Springer, 662–675. doi: 10.1007/BFb0036946.Google Scholar
Shaked, M. and Shanthikumar, G. (2007). Stochastic Orders, Springer.CrossRefGoogle Scholar
Swirszcz, T. (1974). Monadic functors and convexity. Bulletin de l’AcaÉmie Polonaise des Sciences: SÉrie des sciences mathematiques, astronomique et physique 22 (1) 39–42.Google Scholar
TopsØe, F. (1970). Topology and Measure, Springer. doi: 10.1007/BFb0069481.CrossRefGoogle Scholar
van Breugel, F. (2005). The Metric Monad for Probabilistic Nondeterminism. Available at http://www.cse.yorku.ca.Google Scholar
Vickers, S. (2011). A monad of valuation locales. Available at cs.bham.ac.uk/ sjv/Riesz.pdf.Google Scholar
Vietoris, L. (1922). Bereiche zweiter Ordnung. Monatshefte fÜr Mathematik und Physik 32 258–280. German. doi: 10.1007/BF01696886.CrossRefGoogle Scholar
ZÖberlein, V. (1976). Doctrines on 2-categories. Mathematische Zeitschrift 148 267–279. doi: 10.1007/BF01214522.CrossRefGoogle Scholar