No CrossRef data available.
Article contents
Rewriting systems for the surface classification theorem
Published online by Cambridge University Press: 27 May 2010
Abstract
The work reported in this paper refers to Massey's proof of the surface classification theorem based on the standard word-rewriting treatment of surfaces. We arrange this approach into a formal rewriting system 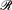 and provide a new version of Massey's argument. Moreover, we study the computational properties of two subsystems of
and provide a new version of Massey's argument. Moreover, we study the computational properties of two subsystems of 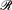 :
: 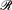 or for dealing with words denoting orientable surfaces and
or for dealing with words denoting orientable surfaces and 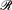 nor for dealing with words denoting non-orientable surfaces. We show how such properties induce an alternative proof for the surface classification in which the basic homeomorphism between the connected sum of three projective planes and the connected sum of a torus with a projective plane is not required.
nor for dealing with words denoting non-orientable surfaces. We show how such properties induce an alternative proof for the surface classification in which the basic homeomorphism between the connected sum of three projective planes and the connected sum of a torus with a projective plane is not required.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2010

