Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T08:22:38.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Specifying Peirce's law in classical realizability

Published online by Cambridge University Press:  17 November 2014

MAURICIO GUILLERMO  and
ALEXANDRE MIQUEL
MAURICIO GUILLERMO
Affiliation:
Centro de Matemática, Facultad de Ciencias, Universidad de la República, Iguá 4225 esq. Mataojo, Montevideo, Uruguay Email: mguille@fing.edu.uy
ALEXANDRE MIQUEL
Affiliation:
Laboratoire d'Informatique du parallélisme, École Normale Supérieure de Lyon 46, allée d'Italie, 69364 Lyon Cedex 07, France
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the specification problem in classical realizability (such as introduced by Krivine (2009 Panoramas et synthéses27)), which is to characterize the universal realizers of a given formula by their computational behaviour. After recalling the framework of classical realizability, we present the problem in the general case and illustrate it with some examples. In the rest of the paper, we focus on Peirce's law, and present two game-theoretic characterizations of its universal realizers. First, we consider the particular case where the language of realizers contains no extra instruction such as ‘quote’ (Krivine 2003 Theoretical Computer Science308 259–276). We present a first game 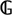$\mathds{G}$0 and show that the universal realizers of Peirce's law can be characterized as the uniform winning strategies for 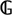$\mathds{G}$0, using the technique of interaction constants. Then we show that in the presence of extra instructions such as ‘quote’, winning strategies for the game 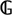$\mathds{G}$0 are still adequate but no more complete. For that, we exhibit an example of a wild realizer of Peirce's law, that introduces a purely game-theoretic form of backtrack that is not captured by 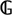$\mathds{G}$0. We finally propose a more sophisticated game 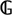$\mathds{G}$1, and show that winning strategies for the game 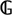$\mathds{G}$1 are both adequate and complete in the general case, without any further assumption about the instruction set used by the language of classical realizers.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 26 , Issue 7 , October 2016 , pp. 1269 - 1303
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barendregt, H. (1984) The Lambda Calculus: Its Syntax and Semantics, Studies in Logic and The Foundations of Mathematics volume 103, North-Holland.Google Scholar
Barbanera, F. and Berardi, S. (1996) A symmetric lambda calculus for classical program extraction. Information and Computation 125 (2) 103–117.Google Scholar
Church, A. (1941) The Calculi of Lambda-Conversion, Annals of Mathematical Studies volume 6, Princeton.Google Scholar
Curien, P.-L. and Herbelin, H. (2000) The duality of computation. In: International Conference on Functional Programming 233–243.Google Scholar
Curry, H. B. and Feys, R. (1958) Combinatory Logic, volume 1, North-Holland.Google Scholar
Friedman, H. (1973) Some applications of Kleene's methods for intuitionistic systems. In: Cambridge Summer School in Mathematical Logic. Springer-Verlag Lecture Notes in Mathematics 337 113–170.Google Scholar
Friedman, H. (1978) Classically and intuitionistically provably recursive functions. Higher Set Theory 669 21–28.CrossRefGoogle Scholar
Girard, J.-Y. (2006) Le point aveugle – Cours de logique – Volume I – vers la perfection, Hermann.Google Scholar
Girard, J.-Y., Lafont, Y. and Taylor, P. (1989) Proofs and Types, Cambridge University Press.Google Scholar
Goldblatt, R. (1985) On the role of the Baire category theorem and dependent choice in the foundations of logic. Journal of Symbolic Logic 50 412–422.Google Scholar
Griffin, T. (1990) A formulae-as-types notion of control. In: Principles of Programming Languages 47–58.Google Scholar
Guillermo, M. (2008) Jeux de réalisabilité en arithmétique classique, Ph.D. thesis, Université Paris 7.Google Scholar
Howard, W. A. (1969) The formulae-as-types notion of construction. Privately circulated notes.Google Scholar
Kleene, S. C. (1945) On the interpretation of intuitionistic number theory. Journal of Symbolic Logic 10 109–124.Google Scholar
Krivine, J. -L. (1993) Lambda-Calculus, Types and Models, Masson.Google Scholar
Krivine, J.-L. (2001) Typed lambda-calculus in classical Zermelo-Fraenkel set theory. Archive for Mathematical Logic 40 (3) 189–205.CrossRefGoogle Scholar
Krivine, J.-L. (2003) Dependent choice, ‘quote’ and the clock. Theoretical Computer Science 308 259–276.CrossRefGoogle Scholar
Krivine, J.-L. (2009) Realizability in classical logic. In: interactive models of computation and program behaviour. Panoramas et synthèses, 27 197–229.Google Scholar
Martin-Löf, P. (1998) An intuitionistic theory of types. In twenty-five years of constructive type theory. Oxford Logic Guides 36 127–172.Google Scholar
McCarty, D. (1984) Realizability and Recursive Mathematics, Ph.D. thesis, Carnegie-Mellon University.Google Scholar
Miquel, A. (2007) Classical program extraction in the calculus of constructions. In: Computer Science Logic, 21st International Workshop, 16th Annual Conference of the EACSL, Lausanne, Switzerland, September 11-15, 2007, Springer Lecture Notes in Computer Science 4646 313–327.CrossRefGoogle Scholar
Miquel, A. (2010) Existential witness extraction in classical realizability and via a negative translation. Logical Methods for Computer Science 7 (2) 1–47.Google Scholar
Myhill, J. (1973) Some properties of intuitionistic Zermelo–Fraenkel set theory. Lecture Notes in Mathematics 337 206–231.Google Scholar
Oliva, P. and Streicher, T. (2008) On Krivine's realizability interpretation of classical second-order arithmetic. Fundamenta Informaticae 84 (2) 207–220.Google Scholar
Parigot, M. (1997) Proofs of strong normalisation for second order classical natural deduction. The Journal of Symbolic Logic 62 (4) 1461–1479.CrossRefGoogle Scholar
Sperber, M., Kent Dybvig, R., Flatt, M., Van Straaten, A., Findler, R. and Matthews, J. (2009) Revised 6 report on the algorithmic language Scheme. Journal of Functional Programming 19 Supplement S1 1–301.CrossRefGoogle Scholar