Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T08:11:04.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Tilings: simulation and universality

Published online by Cambridge University Press:  27 October 2010

GREGORY LAFITTE  and
MICHAEL WEISS
GREGORY LAFITTE
Affiliation:
Laboratoire d'Informatique Fondamentale de Marseille (LIF), CNRS – Aix-Marseille Université, 39 rue Joliot-Curie, F-13453 Marseille Cedex 13, France Email: Gregory.Lafitte@lif.univ-mrs.fr
MICHAEL WEISS
Affiliation:
Laboratoire I3S, CNRS – Université de Nice Sophia-Antipolis, Les Algorithmes, Bât. Euclide B, 2000 route des Lucioles, BP 121, F-06903 Sophia Antipolis Cedex, France Email: Michael.Weiss@unice.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Wang tiles are unit-size squares with coloured edges. In this paper, we approach one aspect of the study of tiling computability: the quest for a universal tile set. Using a complex construction, based on Robinson's classical construction and its different modifications, we build a tile set 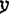(pronounced ayin) that almost always simulates any tile set. By way of Banach–Mazur games on tilings topological spaces, we prove that the set of 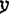-tilings that do not satisfy the universality condition is meagre in the set of 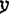-tilings.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 20 , Special Issue 5: Theory and Applications of Models of Computation (TAMC 2008–2009) , October 2010 , pp. 813 - 850
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allauzen, C. and Durand, B. (1997) Appendix A: Tiling problems. In: Börger, E., Grädel, E. and Gurevich, Y. (eds.) The classical decision problem, Springer-Verlag 407–420.Google Scholar
Berger, R. (1966) The undecidability of the domino problem. Mem. Amer. Math Soc. 66 1–72.Google Scholar
Cervelle, J. and Durand, B. (2004) Tilings: recursivity and regularity. Theoretical Computer Science 310 (1-3)469–477.CrossRefGoogle Scholar
Delorme, M., Mazoyer, J., Ollinger, N. and Theyssier, G. (2010) Bulking I: an abstract theory of bulking. Available at http://hal.archives-ouvertes.fr/hal-00451732/fr/.Google Scholar
Durand, B. (1999) Tilings and quasiperiodicity. Theoretical Computer Science 221 (1-2)61–75.CrossRefGoogle Scholar
Durand, B., Levin, L. A. and Shen, A. (2001) Complex tilings. In: Proceedings of the thirty-third annual ACM Symposium on Theory of Computation (STOC), ACM 732–739.CrossRefGoogle Scholar
Durand, B., Levin, L. A. and Shen, A. (2004) Local rules and global order. Mathematical Intelligencer 27 (1)64–68.CrossRefGoogle Scholar
Durand, B., Romashchenko, A. E. and Shen, A. (2008) Fixed point and aperiodic tilings. In: Ito, M. and Toyama, M. (eds.) Proceedings of the conference Developments in Language Theory. Springer-Verlag Lecture Notes in Computer Science 5257 276–288.Google Scholar
Hanf, W. P. (1974) Nonrecursive tilings of the plane. I. Journal of Symbolic Logic 39 (2)283–285.CrossRefGoogle Scholar
Lafitte, G. and Weiss, M. (2007) Universal tilings. In: Thomas, W. and Weil, P. (eds.) Twenty-Fourth International Symposium on Theoretical Aspects of Computer Science (STACS'2007). Springer-Verlag Lecture Notes in Computer Science 4393 367–380.Google Scholar
Lafitte, G. and Weiss, M. (2008a) Computability of tilings. In: Ausiello, G., Karhumäki, J., Mauri, G. and Ong, C.-H. L. (eds.) Proceedings of the Fifth IFIP International Conference on Theoretical Computer Science (IFIP-TCS'2008). IFIP Conference Proceedings, Springer-Verlag 273 187–201.Google Scholar
Lafitte, G. and Weiss, M. (2008b) Simulations between tilings. In: Beckmann, A., Dimitracopoulos, C. and Löwe, B. (eds.) Logic and Theory of Algorithms, Fourth Conference on Computability in Europe (CiE'2008), University of Athens 264–273.Google Scholar
Lafitte, G. and Weiss, M. (2008c) A topological study of tilings. In: Agrawal, M., Du, D., Duan, Z. and Li, A. (eds.), Fifth Annual Conference on Theory and Applications of Models of Computation (TAMC'2008). Springer-Verlag Lecture Notes in Computer Science 4978 375–387.Google Scholar
Lafitte, G. and Weiss, M. (2009) An almost totally universal tile set. In: Chen, J. and Cooper, S. B. (eds.) Sixth Annual Conference on Theory and Applications of Models of Computation (TAMC'2009). Springer-Verlag Lecture Notes in Computer Science 5532 271–280.CrossRefGoogle Scholar
Myers, D. (1974) Nonrecursive tilings of the plane. II. Journal of Symbolic Logic 39 (2)286–294.CrossRefGoogle Scholar
Oxtoby, J. (1957) The Banach–Mazur game and Banach category theorem. In: Contribution to the theory of games, Volume III. Annals of Mathematical Studies, Princeton University Press 39159–163.Google Scholar
Robinson, R. M. (1971) Undecidability and nonperiodicity for tilings of the plane. Inventiones Mathematicae 12 (3)177–209.CrossRefGoogle Scholar
Wang, H. (1961) Proving theorems by pattern recognition II. Bell System Tech. Journal 40 (1)1–41.Google Scholar