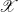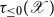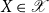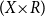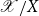1. Introduction
We study categories of modules over a ring in homotopy type theory (HoTT). Our main result is that these satisfy the (internal) axioms AB3 through AB5 and have a generator, meaning they are Grothendieck categories. By working in HoTT, our results hold in any (Grothendieck)
![]() $ \infty $
-topos (Shulman, Reference Shulman2019) and conjecturally (Kapulkin and Lumsdaine, Reference Kapulkin and Lumsdaine2018) in any elementary
$ \infty $
-topos (Shulman, Reference Shulman2019) and conjecturally (Kapulkin and Lumsdaine, Reference Kapulkin and Lumsdaine2018) in any elementary
![]() $\infty$
-topos (Rasekh, Reference Rasekh2022; Shulman, Reference Shulman2017). This work is part of, and motivated by, the development of homological algebra in HoTT and the resulting notions in an
$\infty$
-topos (Rasekh, Reference Rasekh2022; Shulman, Reference Shulman2017). This work is part of, and motivated by, the development of homological algebra in HoTT and the resulting notions in an
![]() $\infty$
-topos, which we discuss in Section 4.
$\infty$
-topos, which we discuss in Section 4.
In ordinary homological algebra, it is common knowledge that the category of modules over a ring is Grothendieck and satisfies AB4. However, the question is more subtle in a constructive setting such as ours. For example, the category of abelian groups in the type theory of Coquand and Spiwack (Reference Coquand, Spiwack, Kauers, Kerber, Miner and Windsteiger2007) is only preabelian (see their Section 4.1 for a discussion). Fortunately for us,
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
is abelian in HoTT, and this has already been formalised for
$ {{R}\textrm{-}{\mathrm{Mod}}} $
is abelian in HoTT, and this has already been formalised for
![]() $ R \equiv {\mathbb{Z}} $
in the file CategoryTheory/categories/abgrs.v of the Voevodsky et al. (https://unimath.org) library.
$ R \equiv {\mathbb{Z}} $
in the file CategoryTheory/categories/abgrs.v of the Voevodsky et al. (https://unimath.org) library.
The main subtlety in verifying that
![]() $ {{R}\textrm{-}{\mathrm{Mod}}}$
is Grothendieck is the existence of coproducts over an arbitrary set X. When assuming the law of the excluded middle, we are accustomed to having a natural monomorphism
$ {{R}\textrm{-}{\mathrm{Mod}}}$
is Grothendieck is the existence of coproducts over an arbitrary set X. When assuming the law of the excluded middle, we are accustomed to having a natural monomorphism
![]() $ \bigoplus_{x:X} A(x) \to \Pi_{x:X} A(x) $
from an arbitrary coproduct of modules to the corresponding product. Indeed, one often defines the coproduct to be the ‘finitely supported’ elements within the product. While the coproduct
$ \bigoplus_{x:X} A(x) \to \Pi_{x:X} A(x) $
from an arbitrary coproduct of modules to the corresponding product. Indeed, one often defines the coproduct to be the ‘finitely supported’ elements within the product. While the coproduct
![]() $ \bigoplus_{x:X} A(x) $
still always exists in a constructive setting, it is harder to define, and in contrast to the classical setting there may be no non-trivial maps (let alone monomorphisms) of the form
$ \bigoplus_{x:X} A(x) $
still always exists in a constructive setting, it is harder to define, and in contrast to the classical setting there may be no non-trivial maps (let alone monomorphisms) of the form
![]() $ \bigoplus_{x:X} A(x) \to \Pi_{x:X} A(x) $
. This is further discussed in Section 3.1.
$ \bigoplus_{x:X} A(x) \to \Pi_{x:X} A(x) $
. This is further discussed in Section 3.1.
When Grothendieck first introduced the AB axioms, he remarked that AB4 follows from AB5 (Grothendieck, Reference Grothendieck1957, p. 129). This is the second point which is a bit more subtle in our setting, and we prove this in Section 3.3. In fact, we prove a bit more: the AB5 axiom implies that the coproduct functor
![]() $ \bigoplus_X $
is left-exact for arbitrary sets X (Theorem 3.3.10). Our result is analogous to, and inspired by, the internal coproduct of a family of abelian groups in an elementary topos (with
$ \bigoplus_X $
is left-exact for arbitrary sets X (Theorem 3.3.10). Our result is analogous to, and inspired by, the internal coproduct of a family of abelian groups in an elementary topos (with
![]() ${\mathbb{N}}$
) as constructed by RoswithaHarting inHarting (Reference Harting1982). Her main result is that the internal coproduct, indexed by an arbitrary object, is left-exact (hence preserves monomorphisms). After Proposition 3.7 in Blechschmidt (Reference Blechschmidt2018), Ingo Blechschmidt remarks that the internal coproduct exists and preserves monomorphisms for families of modules as well. Our work in Section 3.3 simultaneously translates and generalises these results by constructing type-indexed colimits in arbitrary abelian categories in HoTT. We then recover the analogue of Harting’s result: when the indexing type is a set, the colimit specialises to the coproduct and is left-exact. In general, however, the colimit fails to be left-exact (Example 3.2.6).
${\mathbb{N}}$
) as constructed by RoswithaHarting inHarting (Reference Harting1982). Her main result is that the internal coproduct, indexed by an arbitrary object, is left-exact (hence preserves monomorphisms). After Proposition 3.7 in Blechschmidt (Reference Blechschmidt2018), Ingo Blechschmidt remarks that the internal coproduct exists and preserves monomorphisms for families of modules as well. Our work in Section 3.3 simultaneously translates and generalises these results by constructing type-indexed colimits in arbitrary abelian categories in HoTT. We then recover the analogue of Harting’s result: when the indexing type is a set, the colimit specialises to the coproduct and is left-exact. In general, however, the colimit fails to be left-exact (Example 3.2.6).
The original construction of the internal coproduct of abelian groups was carried out in the internal language of an elementary topos. This internal language was not well-developed at the time, and the paper Harting (Reference Harting1982) – which is entirely dedicated to this construction – weighs in at over 60 pages. In contrast, by working in HoTT our generalised construction goes through in just over 2 pages (Section 3.3).
The usual proof that AB5 implies AB4 replaces a discrete indexing category X (for a coproduct) by a filtered category (the finite subsets of X) and uses the fact that moving from one to the other does not change the colimit of a diagram. However, in a constructive setting neither the Bishop-finite nor the (ordered) finite subsets of X form a filtered category unless X is decidable. Harting’s insight was to work with the category HX of lists of elements in X instead. In Section 3.3, we define a precategory HX from a 1-type X in HoTT and then we show that HX is always sifted, and moreover filtered if X is a set. In Section 2, we develop the necessary theory of sifted and filtered colimits.
In Section 4, we interpret our most central results into a higher topos
![]() $ {\mathscr{X}} $
equipped with a ring object R. Specifically, we show that the internal category of R-modules resulting from interpretation represents the presheaf sending an
$ {\mathscr{X}} $
equipped with a ring object R. Specifically, we show that the internal category of R-modules resulting from interpretation represents the presheaf sending an
![]() $ X \in {\mathscr{X}} $
to the category of
$ X \in {\mathscr{X}} $
to the category of
![]() $(X{\times}R)$
-modules over X (Theorem 4.3.4). We repackage internal categories as Rezk (1,1)-objects (Definition 4.1.1), which are 2-restricted versions of 0-truncated complete Segal objects. Rezk (1,1)-objects are easily seen to represent presheaves of categories, which is their main utility for us.
$(X{\times}R)$
-modules over X (Theorem 4.3.4). We repackage internal categories as Rezk (1,1)-objects (Definition 4.1.1), which are 2-restricted versions of 0-truncated complete Segal objects. Rezk (1,1)-objects are easily seen to represent presheaves of categories, which is their main utility for us.
We also interpret type-indexed colimits of modules, which specialise to coproducts when the indexing type is a set. For an object
![]() $ X \in {\mathscr{X}} $
, we get an adjunction
$ X \in {\mathscr{X}} $
, we get an adjunction
![]() $ {\mathrm{colim}_{X}} : {{(X{\times}R)}\textrm{-}{\mathrm{Mod}}} \leftrightarrows {{R}\textrm{-}{\mathrm{Mod}}} : X \times (-) $
where the left adjoint preserves products (Theorem 4.3.5). If X is a set, then the left adjoint is left-exact. To deduce (external) left-exactness from internal left-exactness (resulting from interpretation), we use an internalisation procedure (Definition 4.1.7) that applies more generally and may be of independent interest.
$ {\mathrm{colim}_{X}} : {{(X{\times}R)}\textrm{-}{\mathrm{Mod}}} \leftrightarrows {{R}\textrm{-}{\mathrm{Mod}}} : X \times (-) $
where the left adjoint preserves products (Theorem 4.3.5). If X is a set, then the left adjoint is left-exact. To deduce (external) left-exactness from internal left-exactness (resulting from interpretation), we use an internalisation procedure (Definition 4.1.7) that applies more generally and may be of independent interest.
1.1 Conventions
We use the conventions and notation of The Univalent Foundations Program (2013). Our terminology for category theory mirrors that of The Univalent Foundations Program (2013, Chapter 9) and Ahrens et al. (Reference Ahrens, Kapulkin and Shulman2015), in particular we leave the ‘univalent’ implicit when saying category (except in this paper’s title). When we consider abelian categories, we do assume these are univalent. If
![]() $ \mathscr{D} $
and
$ \mathscr{D} $
and
![]() $ \mathscr{C} $
are precategories, we denote the functor precategory using exponential notation:
$ \mathscr{C} $
are precategories, we denote the functor precategory using exponential notation:
![]() $ \mathscr{C}^{\mathscr{D}} $
. For a functor
$ \mathscr{C}^{\mathscr{D}} $
. For a functor
![]() $ F : \mathscr{C}^\mathscr{D} $
and a morphism
$ F : \mathscr{C}^\mathscr{D} $
and a morphism
![]() $ \delta : d \to d' $
in
$ \delta : d \to d' $
in
![]() $ \mathscr{D} $
, we write
$ \mathscr{D} $
, we write
![]() $ F_\delta : F(d) \to F(d') $
for the morphism in
$ F_\delta : F(d) \to F(d') $
for the morphism in
![]() $ \mathscr{C} $
obtained by applying F. If moreover
$ \mathscr{C} $
obtained by applying F. If moreover
![]() $ \eta : G \Rightarrow G' $
is a natural transformation of functors with domain
$ \eta : G \Rightarrow G' $
is a natural transformation of functors with domain
![]() $ \mathscr{C} $
, then we will write
$ \mathscr{C} $
, then we will write
![]() $ \eta_F $
for the restriction of
$ \eta_F $
for the restriction of
![]() $ \eta $
along F.
$ \eta $
along F.
When we say something is a ‘property of X’, we mean it in the formal sense of being a proposition. The standard n-element set is denoted
![]() ${\mathrm{Fin}(n)}$
. Section 4 has its own section on notation.
${\mathrm{Fin}(n)}$
. Section 4 has its own section on notation.
2 Sifted and Filtered Precategories
We define sifted and filtered precategories and then prove that sifted (resp. filtered) colimits of sets commute with finite products (resp. finite limits). In fact, we prove the stronger fact that filtered colimits commute with finitely generated limits (Definition 2.3.2). This generalisation lets us, for example, compute the fixed points of a filtered colimit of G-sets as the filtered colimit of the fixed points, for a finitely generated group G (Corollary 2.3.7).
These are classical results in category theory, and the usual proofs go through in our context with some added care, which is what we supply. The work builds on Chapters 9 and 10 of the HoTT Book (The Univalent Foundations Program, 2013).
Before we begin, we would like to emphasise that developing 1-category theory in HoTT is unproblematic, as opposed to
![]() $ \infty $
-category theory. We do not know how, or whether it is even possible, to represent current approaches to the latter in HoTT. Nevertheless, we may speak about
$ \infty $
-category theory. We do not know how, or whether it is even possible, to represent current approaches to the latter in HoTT. Nevertheless, we may speak about
![]() $ \infty $
-groupoids and functors between them, namely: an
$ \infty $
-groupoids and functors between them, namely: an
![]() $ \infty $
-groupoid is simply a type, and a functor is simply a function. In particular, if X is a type and
$ \infty $
-groupoid is simply a type, and a functor is simply a function. In particular, if X is a type and
![]() $ \mathscr{C} $
is a category, then a function
$ \mathscr{C} $
is a category, then a function
![]() $ X \to \mathscr{C} $
is a functor from this point of view, and there is an obvious category
$ X \to \mathscr{C} $
is a functor from this point of view, and there is an obvious category
![]() $ \mathscr{C}^X $
.
$ \mathscr{C}^X $
.
2.1 Limits and colimits of sets
We start by defining limits and colimits indexed by precategories. When the codomain is a category, we show that the (co)limit of a functor is invariant under replacing the domain with its Rezk completion (Lemma 2.1.3). For limits and colimits of sets, we show that the classical descriptions remain valid in our setting (Proposition 2.1.4). Lastly, when the indexing category is a groupoid (i.e., a 1-type; see The Univalent Foundations Program 2013, Example 9.1.16), we show that the limit and colimit are given, respectively, by the
![]() $ \Pi $
- and
$ \Pi $
- and
![]() $ \Sigma $
-type of the underlying family (Proposition 2.1.6).
$ \Sigma $
-type of the underlying family (Proposition 2.1.6).
Definition 2.1.1 Let
![]() $ D : \mathscr{D} \to \mathscr{C} $
be a functor between precategories. A limit of D is an object
$ D : \mathscr{D} \to \mathscr{C} $
be a functor between precategories. A limit of D is an object
![]() $ {\mathrm{lim}_{\mathscr{D}}}\, D $
of
$ {\mathrm{lim}_{\mathscr{D}}}\, D $
of
![]() $ \mathscr{C} $
representing the functor
$ \mathscr{C} $
representing the functor
![]() $ \mathscr{C}^{\mathscr{D}} ({\mathrm{const}_{\mathscr{D}}}(-), D) : \mathscr{C}^{\mathrm{op}} \to \mathrm{Set} $
. Dually, a colimit of D is an object
$ \mathscr{C}^{\mathscr{D}} ({\mathrm{const}_{\mathscr{D}}}(-), D) : \mathscr{C}^{\mathrm{op}} \to \mathrm{Set} $
. Dually, a colimit of D is an object
![]() $ {\mathrm{colim}_{\mathscr{D}}}\, D $
of
$ {\mathrm{colim}_{\mathscr{D}}}\, D $
of
![]() $ \mathscr{C} $
representing the functor
$ \mathscr{C} $
representing the functor
![]() $ \mathscr{C}^{\mathscr{D}}(D, {\mathrm{const}_{\mathscr{D}}}(-)) $
.
$ \mathscr{C}^{\mathscr{D}}(D, {\mathrm{const}_{\mathscr{D}}}(-)) $
.
When
![]() $ \mathscr{C} $
is a category, Theorem 9.5.9 in The Univalent Foundations Program (2013) implies that the type of (co)limits of a functor D is a mere proposition. Thus if a (co)limit exists, it is unique.
$ \mathscr{C} $
is a category, Theorem 9.5.9 in The Univalent Foundations Program (2013) implies that the type of (co)limits of a functor D is a mere proposition. Thus if a (co)limit exists, it is unique.
Remark 2.1.2 Consider a functor
![]() $ D : \mathscr{D} \to \mathscr{C} $
. The datum of a limit of D consists of an object
$ D : \mathscr{D} \to \mathscr{C} $
. The datum of a limit of D consists of an object
![]() $ {\mathrm{lim}_{\mathscr{D}}}\, D : \mathscr{C} $
along with a natural isomorphism
$ {\mathrm{lim}_{\mathscr{D}}}\, D : \mathscr{C} $
along with a natural isomorphism
![]() $ \delta : \mathscr{C}^\mathscr{D}({\mathrm{const}_{\mathscr{D}}}(-), D) \simeq \mathscr{C}(-, {\mathrm{lim}_{\mathscr{D}}}\, D) $
witnessing representability. When we say that an object
$ \delta : \mathscr{C}^\mathscr{D}({\mathrm{const}_{\mathscr{D}}}(-), D) \simeq \mathscr{C}(-, {\mathrm{lim}_{\mathscr{D}}}\, D) $
witnessing representability. When we say that an object
![]() $ c : \mathscr{C} $
‘is the limit of D ’, we mean that such a representability witness is specified. Of course, by the Yoneda lemma, such a witness consists exactly of an element in
$ c : \mathscr{C} $
‘is the limit of D ’, we mean that such a representability witness is specified. Of course, by the Yoneda lemma, such a witness consists exactly of an element in
![]() $ \mathscr{C}^\mathscr{D}({\mathrm{const}_{\mathscr{D}}}(c), D) $
defining a universal cocone on D. The dual story applies to colimits.
$ \mathscr{C}^\mathscr{D}({\mathrm{const}_{\mathscr{D}}}(c), D) $
defining a universal cocone on D. The dual story applies to colimits.
Given a functor
![]() $ D : \mathscr{D} \to \mathscr{C} $
from a precategory to a category, we may factor D uniquely via the Rezk completion
$ D : \mathscr{D} \to \mathscr{C} $
from a precategory to a category, we may factor D uniquely via the Rezk completion
![]() $ {\widehat{\mathscr{D}}} $
as follows (see The Univalent Foundations Program 2013, Chapter 9.9 for details):
$ {\widehat{\mathscr{D}}} $
as follows (see The Univalent Foundations Program 2013, Chapter 9.9 for details):

In particular, we have a natural comparison map
![]() $ {\mathrm{lim}_{{\widehat{\mathscr{D}}}}}\, \widehat{D} \longrightarrow {\mathrm{lim}_{\mathscr{D}}}\, D $
induced from
$ {\mathrm{lim}_{{\widehat{\mathscr{D}}}}}\, \widehat{D} \longrightarrow {\mathrm{lim}_{\mathscr{D}}}\, D $
induced from
![]() $ \eta_{\mathscr{D}} $
by precomposition, and dually for the colimit. The following lemma implies that that these comparison maps are isomorphisms, meaning we can freely move between the (co)limit of D and
$ \eta_{\mathscr{D}} $
by precomposition, and dually for the colimit. The following lemma implies that that these comparison maps are isomorphisms, meaning we can freely move between the (co)limit of D and
![]() $ \widehat{D} $
.
$ \widehat{D} $
.
Lemma 2.1.3 Let
![]() $ D : \mathscr{D} \to \mathscr{C} $
be a functor from a precategory to a category. The restriction maps
$ D : \mathscr{D} \to \mathscr{C} $
be a functor from a precategory to a category. The restriction maps
are bijections natural in
![]() $ c : \mathscr{C} $
. Consequently, the (co)limits of D and
$ c : \mathscr{C} $
. Consequently, the (co)limits of D and
![]() $ \widehat{D} $
coincide, if either exists.
$ \widehat{D} $
coincide, if either exists.
Proof. The functor
![]() $ \eta_{\mathscr{D}} : \mathscr{D} \to {\widehat{\mathscr{D}}} $
is a weak equivalence (The Univalent Foundations Program, 2013, Theorem 9.9.5), thus mapping into
$ \eta_{\mathscr{D}} : \mathscr{D} \to {\widehat{\mathscr{D}}} $
is a weak equivalence (The Univalent Foundations Program, 2013, Theorem 9.9.5), thus mapping into
![]() $ \mathscr{C} $
induces an isomorphism
$ \mathscr{C} $
induces an isomorphism
![]() $ \eta_{\mathscr{D}}^* : \mathscr{C}^{{\widehat{\mathscr{D}}}} \to \mathscr{C}^{\mathscr{D}} $
by The
$ \eta_{\mathscr{D}}^* : \mathscr{C}^{{\widehat{\mathscr{D}}}} \to \mathscr{C}^{\mathscr{D}} $
by The
Univalent Foundations Program (2013, Theorem 9.9.4). Clearly, for every
![]() $ c : \mathscr{C} $
, we have that
$ c : \mathscr{C} $
, we have that
![]() $ {\mathrm{const}_{{\widehat{\mathscr{D}}}}}(c) \circ \eta_{\mathscr{D}} = {\mathrm{const}_{\mathscr{D}}}(c) $
and
$ {\mathrm{const}_{{\widehat{\mathscr{D}}}}}(c) \circ \eta_{\mathscr{D}} = {\mathrm{const}_{\mathscr{D}}}(c) $
and
![]() $ \widehat{D} \circ \eta_{\mathscr{D}} = D $
by definition. The maps in question are actions of
$ \widehat{D} \circ \eta_{\mathscr{D}} = D $
by definition. The maps in question are actions of
![]() $ \eta_{\mathscr{D}}^* : \mathscr{C}^{{\widehat{\mathscr{D}}}} \to \mathscr{C}^{\mathscr{D}} $
on specific hom-sets, which are (natural) bijections by full faithfulness.
$ \eta_{\mathscr{D}}^* : \mathscr{C}^{{\widehat{\mathscr{D}}}} \to \mathscr{C}^{\mathscr{D}} $
on specific hom-sets, which are (natural) bijections by full faithfulness.
The usual descriptions of limits and colimits of sets are valid in HoTT.
Proposition 1.4 Let
![]() $ \mathscr{D} $
be a small category, and
$ \mathscr{D} $
be a small category, and
![]() $ D : \mathscr{D} \to \mathrm{Set} $
a functor.
$ D : \mathscr{D} \to \mathrm{Set} $
a functor.
-
(1) The limit of D exists and is given by the set
equipped with the natural projections \[ {\mathrm{lim}_{\mathscr{D}}}\, D = \{ x : \Pi_{\mathscr{D}} D \mid \Pi_{d,d' : \mathscr{D}} \Pi_{\delta : d \to d'} D_\delta (x_d) = x_{d'} \} \]
\[ {\mathrm{lim}_{\mathscr{D}}}\, D = \{ x : \Pi_{\mathscr{D}} D \mid \Pi_{d,d' : \mathscr{D}} \Pi_{\delta : d \to d'} D_\delta (x_d) = x_{d'} \} \]
 $ ({\mathrm{lim}_{\mathscr{D}}}\, D \to D(d))_{d : \mathscr{D}} $
forming a universal cocone.
$ ({\mathrm{lim}_{\mathscr{D}}}\, D \to D(d))_{d : \mathscr{D}} $
forming a universal cocone.
-
(2) The colimit of D also exists and is given by the set-quotient of
 $ \Sigma_{\mathscr{D}} D $
by the relation equipped with the natural quotient maps
$ \Sigma_{\mathscr{D}} D $
by the relation equipped with the natural quotient maps \[ (d, x) \sim (d', x') := {\lVert { \Sigma_{\delta : d \to d'} D_\delta (x) = x' } \lVert } \]
\[ (d, x) \sim (d', x') := {\lVert { \Sigma_{\delta : d \to d'} D_\delta (x) = x' } \lVert } \]
 $ (D(d) \to \Sigma_{\mathscr{D}} D / {\sim} )_{d : \mathscr{D}} $
forming a universal cocone.
$ (D(d) \to \Sigma_{\mathscr{D}} D / {\sim} )_{d : \mathscr{D}} $
forming a universal cocone.
Proof. The description of the limit (1) results from computing
![]() $ {\mathrm{lim}_{\mathscr{D}}}\, D $
via products and equalisers:
$ {\mathrm{lim}_{\mathscr{D}}}\, D $
via products and equalisers:
By the explicit descriptions of products and equalisers in
![]() $ \mathrm{Set} $
, we are done. Dually, the description of colimits (2) is obtained by writing
$ \mathrm{Set} $
, we are done. Dually, the description of colimits (2) is obtained by writing
![]() $ {\mathrm{colim}_{D}}\, D $
via coproducts and coequalisers and using their respective descriptions as
$ {\mathrm{colim}_{D}}\, D $
via coproducts and coequalisers and using their respective descriptions as
![]() $ \Sigma $
-types and quotients in
$ \Sigma $
-types and quotients in
![]() $ \mathrm{Set} $
.
$ \mathrm{Set} $
.
For indexing categories which are groupoids, both limits and colimits have a simpler description, given in Proposition 2.1.6. To show this, we use the following lemma, which tells us that for functors from a groupoid into a category, we can choose to simply work with the underlying map of types.
Lemma 2.1.5 Let
![]() $ \mathscr{G} $
be a groupoid, and
$ \mathscr{G} $
be a groupoid, and
![]() $ \mathscr{C} $
a category. The forgetful map
$ \mathscr{C} $
a category. The forgetful map
![]() $ U : \mathscr{C}^{\mathscr{G}} \to (\mathscr{G} \to \mathscr{C}) $
which forgets functoriality is an equivalence. The inverse V sends a map
$ U : \mathscr{C}^{\mathscr{G}} \to (\mathscr{G} \to \mathscr{C}) $
which forgets functoriality is an equivalence. The inverse V sends a map
![]() $ f : \mathscr{G} \to \mathscr{C} $
to the functor V(f) acting as f on objects, and which sends a path
$ f : \mathscr{G} \to \mathscr{C} $
to the functor V(f) acting as f on objects, and which sends a path
![]() $ \gamma : g =_{\mathscr{G}} g' $
to
$ \gamma : g =_{\mathscr{G}} g' $
to
![]() $ {\mathrm{idtoiso}_{\mathscr{G}}}({\mathrm{ap}}_f(\gamma)) $
.
$ {\mathrm{idtoiso}_{\mathscr{G}}}({\mathrm{ap}}_f(\gamma)) $
.
Proof. First of all, the reader should convince themselves that the proposed definition of the inverse V indeed constructs a functor V(f) from a general map of types
![]() $ f : \mathscr{G} \to \mathscr{C} $
. It is then clear that V is a section of the forgetful map U, so it remains to show that any functor
$ f : \mathscr{G} \to \mathscr{C} $
. It is then clear that V is a section of the forgetful map U, so it remains to show that any functor
![]() $ F : \mathscr{G} \to \mathscr{C} $
is equal to the functor induced from its map on the underlying types.
$ F : \mathscr{G} \to \mathscr{C} $
is equal to the functor induced from its map on the underlying types.
Clearly forgetting functoriality of F and then inducing functoriality produces the same map on the underlying types, by definition. Consider a general map
![]() $ {\mathrm{idtoiso}_{\mathscr{G}}}(\gamma) : g \to g' $
in
$ {\mathrm{idtoiso}_{\mathscr{G}}}(\gamma) : g \to g' $
in
![]() $ \mathscr{G} $
, where
$ \mathscr{G} $
, where
![]() $ \gamma : g =_{\mathscr{G}} g' $
. This is general since
$ \gamma : g =_{\mathscr{G}} g' $
. This is general since
![]() $ \mathscr{G} $
is a groupoid. We need to show that
$ \mathscr{G} $
is a groupoid. We need to show that
![]() $ F_{{\mathrm{idtoiso}_{\mathscr{G}}}(\gamma)} = {\mathrm{idtoiso}_{\mathscr{G}}}({\mathrm{ap}}_F(\gamma)) $
as morphisms
$ F_{{\mathrm{idtoiso}_{\mathscr{G}}}(\gamma)} = {\mathrm{idtoiso}_{\mathscr{G}}}({\mathrm{ap}}_F(\gamma)) $
as morphisms
![]() $ F(g) \to F(g') $
in
$ F(g) \to F(g') $
in
![]() $ \mathscr{C} $
. But this follows by path induction on
$ \mathscr{C} $
. But this follows by path induction on
![]() $ \gamma $
.
$ \gamma $
.
Similar in spirit to Lemma 2.1.3, the following proposition says that a (co)limit of sets is invariant under the change of perspective afforded by the previous lemma.
Proposition 2.1.6 Suppose
![]() $ \mathscr{G} $
is a groupoid, and let
$ \mathscr{G} $
is a groupoid, and let
![]() $ D : \mathscr{G} \to \mathrm{Set} $
be a functor. The natural maps
$ D : \mathscr{G} \to \mathrm{Set} $
be a functor. The natural maps
![]() $ {\mathrm{lim}_{\mathscr{G}}} \,\,D \to \Pi_{\mathscr{G}} D $
and
$ {\mathrm{lim}_{\mathscr{G}}} \,\,D \to \Pi_{\mathscr{G}} D $
and
![]() $ {\lVert {\Sigma_{\mathscr{G}} D} \lVert }_0 \to {\mathrm{colim}_{\mathscr{D}}}\, D $
are bijections.
$ {\lVert {\Sigma_{\mathscr{G}} D} \lVert }_0 \to {\mathrm{colim}_{\mathscr{D}}}\, D $
are bijections.
Proof. First we consider the limit. A family
![]() $ d : \Pi_{\mathscr{G}} D $
lies in the limit if and only if the proposition
$ d : \Pi_{\mathscr{G}} D $
lies in the limit if and only if the proposition
holds. Since
![]() $ \mathscr{G} $
is a groupoid, we can identify
$ \mathscr{G} $
is a groupoid, we can identify
![]() $ \mathscr{G}(g,g') $
with
$ \mathscr{G}(g,g') $
with
![]() $ g =_{\mathscr{G}} g' $
. The above then immediately follows by path induction, meaning the predicate defining the limit is a tautology.
$ g =_{\mathscr{G}} g' $
. The above then immediately follows by path induction, meaning the predicate defining the limit is a tautology.
Similarly, we will show that the equivalence relation defining the colimit is trivial so that the set-quotient on
![]() $ \Sigma_{\mathscr{G}} D $
is simply given by set-truncation. Suppose
$ \Sigma_{\mathscr{G}} D $
is simply given by set-truncation. Suppose
![]() $ (g_0,d_0) \sim (g_1, d_1) $
for the colimit relation defined in Proposition 2.1.4. By definition, there merely exists some
$ (g_0,d_0) \sim (g_1, d_1) $
for the colimit relation defined in Proposition 2.1.4. By definition, there merely exists some
![]() $ f : g_0 \to g_1 $
such that
$ f : g_0 \to g_1 $
such that
![]() $ D_f(d_0) = d_1 $
. We wish to deduce that
$ D_f(d_0) = d_1 $
. We wish to deduce that
![]() $ (g_0, d_0) = (g_1, d_1) $
. Since this is a proposition, we may assume f actually exists. As before, we identify f with a path
$ (g_0, d_0) = (g_1, d_1) $
. Since this is a proposition, we may assume f actually exists. As before, we identify f with a path
![]() $ g_0 =_{\mathscr{G}} g_1$
, using that
$ g_0 =_{\mathscr{G}} g_1$
, using that
![]() $ \mathscr{G} $
is a groupoid. Then the existence of the path
$ \mathscr{G} $
is a groupoid. Then the existence of the path
![]() $ D_f(d_0) = d_1 $
implies exactly that
$ D_f(d_0) = d_1 $
implies exactly that
![]() $ (g_0, d_0) = (g_1, d_1) $
, by the characterisation of paths in
$ (g_0, d_0) = (g_1, d_1) $
, by the characterisation of paths in
![]() $ \Sigma $
-types. In conclusion, the colimit relation
$ \Sigma $
-types. In conclusion, the colimit relation
![]() $ \sim $
is just equality; hence, the set-quotient
$ \sim $
is just equality; hence, the set-quotient
![]() $ {\mathrm{colim}_{\mathscr{G}}} \,D $
is simply
$ {\mathrm{colim}_{\mathscr{G}}} \,D $
is simply
![]() $ {\lVert {\Sigma_{\mathscr{G}} D} \lVert }_0 $
.
$ {\lVert {\Sigma_{\mathscr{G}} D} \lVert }_0 $
.
2.2 Sifted colimits
We define sifted precategories and prove that sifted colimits commute with finite products in
![]() $ \mathrm{Set} $
. In Adámek et al. (Reference Adámek, Rosický and Vitale2010), sifted categories are defined to have this property. We will instead take the equivalent condition of Theorem 2.15 from loc. cit. as our definition, which is a simpler condition to check. To us, the main interest is that sifted colimits of algebraic structures (such as groups, abelian groups and modules) may be computed on the underlying sets – see Corollary 2.2.6.
$ \mathrm{Set} $
. In Adámek et al. (Reference Adámek, Rosický and Vitale2010), sifted categories are defined to have this property. We will instead take the equivalent condition of Theorem 2.15 from loc. cit. as our definition, which is a simpler condition to check. To us, the main interest is that sifted colimits of algebraic structures (such as groups, abelian groups and modules) may be computed on the underlying sets – see Corollary 2.2.6.
Definition 2.2.1 Let
![]() $ \mathscr{C} $
be precategory.
$ \mathscr{C} $
be precategory.
-
(1) Let c and c’ be objects of
 $ \mathscr{C}$
and let
$ \mathscr{C}$
and let
 $ n : {\mathbb{N}} $
. A zig-zag from c to c’ of length n is inductively defined as a path
$ n : {\mathbb{N}} $
. A zig-zag from c to c’ of length n is inductively defined as a path
 $ c =_{\mathscr{C}} c' $
when
$ c =_{\mathscr{C}} c' $
when
 $n \equiv 0$
, and for
$n \equiv 0$
, and for
 $ n \geq 1$
a sequence where ‘
$ n \geq 1$
a sequence where ‘
 $\cdots$
’ signifies a length
$\cdots$
’ signifies a length
 $n-1$
zig-zag from
$n-1$
zig-zag from
 $c_2$
to c’ (hence just a path if
$c_2$
to c’ (hence just a path if
 $n \equiv 1$
).
$n \equiv 1$
).
-
(2) The precategory
 $ \mathscr{C} $
is connected if it is merely inhabited (meaning the proposition
$ \mathscr{C} $
is connected if it is merely inhabited (meaning the proposition
 $ {\lVert {\mathscr{C}}\lVert } $
holds) and for every two objects in
$ {\lVert {\mathscr{C}}\lVert } $
holds) and for every two objects in
 $ \mathscr{C} $
there merely exists a zig-zag connecting them.
$ \mathscr{C} $
there merely exists a zig-zag connecting them.
-
(3) Let
 $ \mathscr{C}' $
be a precategory. A functor
$ \mathscr{C}' $
be a precategory. A functor
 $ F : \mathscr{C}' \to \mathscr{C} $
between precategories is final if for every
$ F : \mathscr{C}' \to \mathscr{C} $
between precategories is final if for every
 $ c : \mathscr{C} $
, the slice precategory
$ c : \mathscr{C} $
, the slice precategory
 $ c / F $
is connected.
$ c / F $
is connected.
Being connected is a property of a precategory, and consequently being final is a property of a functor. In Adámek et al. (Reference Adámek, Rosický and Vitale2010), a functor is said to be final if restriction along it preserves colimits. We have instead taken the equivalent condition (3) of Lemma 2.13 in loc. cit. as our definition, from which we prove this fact:
Proposition 2.2.2 Let
![]() $ F : \mathscr{C}' \to \mathscr{C} $
and
$ F : \mathscr{C}' \to \mathscr{C} $
and
![]() $ G : \mathscr{C} \to \mathscr{D} $
be functors between precategories. If F is final, then restriction along F is a natural bijection between functors
$ G : \mathscr{C} \to \mathscr{D} $
be functors between precategories. If F is final, then restriction along F is a natural bijection between functors
![]() $ \mathscr{D} \to \mathrm{Set} $
as follows:
$ \mathscr{D} \to \mathrm{Set} $
as follows:
naturally in
![]() $ d : \mathscr{D} $
. Consequently, the colimit of G coincides with the colimit of GF, if either exists.
$ d : \mathscr{D} $
. Consequently, the colimit of G coincides with the colimit of GF, if either exists.
Proof. Let
![]() $ d : \mathscr{D} $
. First of all, it is straightforward to check that
$ d : \mathscr{D} $
. First of all, it is straightforward to check that
![]() $ F^* $
defines a natural transformation as stated. To prove that it is a natural isomorphism, we show that each component is a bijection.
$ F^* $
defines a natural transformation as stated. To prove that it is a natural isomorphism, we show that each component is a bijection.
Injectivity: Suppose
![]() $ \eta, \eta' : G \Rightarrow {\mathrm{const}}_{\mathscr{C}}(d) $
are such that
$ \eta, \eta' : G \Rightarrow {\mathrm{const}}_{\mathscr{C}}(d) $
are such that
![]() $ \eta_F = \eta'_F $
. We want to show that
$ \eta_F = \eta'_F $
. We want to show that
![]() $ \eta_c = \eta'_c $
for all
$ \eta_c = \eta'_c $
for all
![]() $ c : \mathscr{C} $
, which is a proposition. Let
$ c : \mathscr{C} $
, which is a proposition. Let
![]() $ c : \mathscr{C} $
, and pick a morphism
$ c : \mathscr{C} $
, and pick a morphism
![]() $ f : c \to F(c') $
using that
$ f : c \to F(c') $
using that
![]() $ c / F $
is merely inhabited and the fact that we are proving a proposition. But then, by naturality of
$ c / F $
is merely inhabited and the fact that we are proving a proposition. But then, by naturality of
![]() $ \eta $
and
$ \eta $
and
![]() $ \eta' $
, we have
$ \eta' $
, we have
where the middle equation comes from
![]() $ \eta_F = \eta'_F $
. Hence,
$ \eta_F = \eta'_F $
. Hence,
![]() $ F^* $
is injective.
$ F^* $
is injective.
Surjectivity: Consider a natural transformation
![]() $ \nu : GF \Rightarrow {\mathrm{const}_{\mathscr{C}'}}(d) $
. For
$ \nu : GF \Rightarrow {\mathrm{const}_{\mathscr{C}'}}(d) $
. For
![]() $ c : \mathscr{C}$
, define the function
$ c : \mathscr{C}$
, define the function
where
![]() $ f : c \to F(c') $
. For
$ f : c \to F(c') $
. For
![]() $ f, f' : c / F $
, one can easily show (using naturality of
$ f, f' : c / F $
, one can easily show (using naturality of
![]() $ \nu $
) that
$ \nu $
) that
![]() $ \phi(f) = \phi(f') $
by induction over the length of a zig-zag from f to f’. Consequently,
$ \phi(f) = \phi(f') $
by induction over the length of a zig-zag from f to f’. Consequently,
![]() $ {\mathrm{im}({\phi})} $
is a proposition and we may therefore factor
$ {\mathrm{im}({\phi})} $
is a proposition and we may therefore factor
![]() $ \phi $
via its propositional truncation, producing
$ \phi $
via its propositional truncation, producing
![]() $ ptr{\phi} : {\lVert {c / F}\lVert } \to {\mathrm{im}({\phi})} \to (G(c) \to d) $
. (This argument also appears in Kraus et al. Reference Kraus, Escardó, Coquand and Altenkirch2017, Theorem 5.4, which may be consulted for details.) Thus, we get a map
$ ptr{\phi} : {\lVert {c / F}\lVert } \to {\mathrm{im}({\phi})} \to (G(c) \to d) $
. (This argument also appears in Kraus et al. Reference Kraus, Escardó, Coquand and Altenkirch2017, Theorem 5.4, which may be consulted for details.) Thus, we get a map
![]() $ g : G(c) \to d $
using the fact that
$ g : G(c) \to d $
using the fact that
![]() $ c / F $
is merely inhabited. Doing this for all
$ c / F $
is merely inhabited. Doing this for all
![]() $ c : \mathscr{C} $
gets us a transformation
$ c : \mathscr{C} $
gets us a transformation
![]() $ \eta : \Pi_{c : \mathscr{C}} G(c) \to d $
which, by construction, satisfies
$ \eta : \Pi_{c : \mathscr{C}} G(c) \to d $
which, by construction, satisfies
![]() $ \eta_F = \nu $
.
$ \eta_F = \nu $
.
It remains to prove that
![]() $ \eta $
is natural. Let
$ \eta $
is natural. Let
![]() $ g : c_0 \to c_1 $
be a morphism in
$ g : c_0 \to c_1 $
be a morphism in
![]() $ \mathscr{C} $
. We need to show that
$ \mathscr{C} $
. We need to show that
![]() $ \eta_{c_0} = \eta_{c_1} \circ G_g $
, which is a proposition. By finality of F, we may choose
$ \eta_{c_0} = \eta_{c_1} \circ G_g $
, which is a proposition. By finality of F, we may choose
![]() $ f_0 : c_0 \to F(c'_0) $
and
$ f_0 : c_0 \to F(c'_0) $
and
![]() $ f_1 : c_1 \to F(c'_1) $
to obtain the following diagram:
$ f_1 : c_1 \to F(c'_1) $
to obtain the following diagram:

where the outer diagram is the one we wish to show commutes. Since
![]() $ c_0 / F $
is connected, the two maps
$ c_0 / F $
is connected, the two maps
![]() $ f_0 $
and
$ f_0 $
and
![]() $ f_1 \circ g $
are connected by a zig-zag which, after applying G, produces the dotted lines above. The left square then commutes by definition of a zig-zag, and the triangles on the right commute by naturality of
$ f_1 \circ g $
are connected by a zig-zag which, after applying G, produces the dotted lines above. The left square then commutes by definition of a zig-zag, and the triangles on the right commute by naturality of
![]() $ \nu $
. Inducting over the length of the zig-zag, we conclude that
$ \nu $
. Inducting over the length of the zig-zag, we conclude that
![]() $ \eta $
is natural, as desired.
$ \eta $
is natural, as desired.
Definition 2.2.3 A precategory
![]() $ \mathscr{S} $
is sifted if it is merely inhabited and
$ \mathscr{S} $
is sifted if it is merely inhabited and
![]() $ {\Delta_{\mathscr{S}}} : \mathscr{S} \to \mathscr{S} \times \mathscr{S} $
is final.
$ {\Delta_{\mathscr{S}}} : \mathscr{S} \to \mathscr{S} \times \mathscr{S} $
is final.
There are various equivalent classical definitions of siftedness (see, e.g., Adámek and Rosický Reference Adámek and Rosický2001, Theorem 1.6). We chose the one above to make the connection with final functors immediate and to facilitate the proof of the following:
Lemma 2.2.4 If a precategory
![]() $ \mathscr{C} $
is merely inhabited and has binary coproducts, then
$ \mathscr{C} $
is merely inhabited and has binary coproducts, then
![]() $ \mathscr{C} $
is sifted.
$ \mathscr{C} $
is sifted.
Proof. Suppose
![]() $ \mathscr{C} $
is merely inhabited and has binary coproducts. Then for every
$ \mathscr{C} $
is merely inhabited and has binary coproducts. Then for every
![]() $ (c_0, c_1) : \mathscr{C}^2 $
, the slice precategory
$ (c_0, c_1) : \mathscr{C}^2 $
, the slice precategory
![]() $ (c_0, c_1) / {\Delta_{\mathscr{C}}} $
has an initial object given by the coproduct. Then we are done, since any category with initial object is connected (by zig-zags of length at most 2).
$ (c_0, c_1) / {\Delta_{\mathscr{C}}} $
has an initial object given by the coproduct. Then we are done, since any category with initial object is connected (by zig-zags of length at most 2).
This is one direction of Adámek et al. (Reference Adámek, Rosický and Vitale2010, Theorem 2.15).
Proposition 2.2.5 Sifted colimits of sets commute with finite products.
Proof. Let
![]() $ \mathscr{S} $
be a sifted precategory. The claim that colimits over
$ \mathscr{S} $
be a sifted precategory. The claim that colimits over
![]() $ \mathscr{S} $
commute with empty products follows from
$ \mathscr{S} $
commute with empty products follows from
![]() $ \mathscr{S} $
being merely inhabited. Consider two functors
$ \mathscr{S} $
being merely inhabited. Consider two functors
![]() $ G, H : \mathscr{S} \to \mathrm{Set} $
, then we have the following natural bijections:
$ G, H : \mathscr{S} \to \mathrm{Set} $
, then we have the following natural bijections:
 \begin{align*} {\mathrm{colim}_{s : \mathscr{S}}}\, \big ( G_s \times H_s \big ) &\simeq {\mathrm{colim}_{(s,t): S \times S}}\, G_s \times H_t &\textrm{(Proposition 2.2.2 applied to $ {\Delta_{\mathscr{S}}} $)} \\ &\simeq {\mathrm{colim}_{s : \mathscr{S}}}\, {\mathrm{colim}_{t : \mathscr{S}}}\, G_s \times H_t \\ &\simeq {\mathrm{colim}_{s : \mathscr{S}}}\, \big ( G_s \times {\mathrm{colim}_{t : \mathscr{S}}}\, H_t \big ) &\textrm{($ G_s \times - $ is cocontinuous)} \\ &\simeq {\mathrm{colim}_{s : \mathscr{S}}}\, G_s \times {\mathrm{colim}_{t : \mathscr{S}}}\, H_t &\textrm{( $ - \times {\mathrm{colim}_{t : \mathscr{S}}}\, H_t $ is cocontinuous)} \end{align*}
\begin{align*} {\mathrm{colim}_{s : \mathscr{S}}}\, \big ( G_s \times H_s \big ) &\simeq {\mathrm{colim}_{(s,t): S \times S}}\, G_s \times H_t &\textrm{(Proposition 2.2.2 applied to $ {\Delta_{\mathscr{S}}} $)} \\ &\simeq {\mathrm{colim}_{s : \mathscr{S}}}\, {\mathrm{colim}_{t : \mathscr{S}}}\, G_s \times H_t \\ &\simeq {\mathrm{colim}_{s : \mathscr{S}}}\, \big ( G_s \times {\mathrm{colim}_{t : \mathscr{S}}}\, H_t \big ) &\textrm{($ G_s \times - $ is cocontinuous)} \\ &\simeq {\mathrm{colim}_{s : \mathscr{S}}}\, G_s \times {\mathrm{colim}_{t : \mathscr{S}}}\, H_t &\textrm{( $ - \times {\mathrm{colim}_{t : \mathscr{S}}}\, H_t $ is cocontinuous)} \end{align*}
where the second step can be checked directly. The product bifunctor
![]() $ \times $
preserves colimits in each variable, being a left adjoint.
$ \times $
preserves colimits in each variable, being a left adjoint.
We deduce that sifted colimits of groups and modules can be computed on the underlying sets. This is true more generally for any algebraic theory (Adámek et al., Reference Adámek, Rosický and Vitale2010, Proposition 2.5), but we only state and prove the case that we require.
Corollary 2.6 Let
![]() $\mathscr{A}$
be the category of groups or of R-modules (for a ring R). The forgetful functor
$\mathscr{A}$
be the category of groups or of R-modules (for a ring R). The forgetful functor
![]() $U : \mathscr{A} \to \mathrm{Set}$
creates sifted colimits.
$U : \mathscr{A} \to \mathrm{Set}$
creates sifted colimits.
Proof. We first consider the case when
![]() $\mathscr{A}$
is the category of groups. Let
$\mathscr{A}$
is the category of groups. Let
![]() $\mathscr{S}$
be a sifted precategory and let
$\mathscr{S}$
be a sifted precategory and let
![]() $G : \mathscr{S} \to \mathscr{A}$
be a diagram. The previous proposition implies that the functor
$G : \mathscr{S} \to \mathscr{A}$
be a diagram. The previous proposition implies that the functor
![]() $ {\mathrm{colim}_{\mathscr{S}}} : \mathrm{Set}^{\mathscr{S}} \to \mathrm{Set} $
preserves finite products. It follows that it preserves group objects. Since a group object in
$ {\mathrm{colim}_{\mathscr{S}}} : \mathrm{Set}^{\mathscr{S}} \to \mathrm{Set} $
preserves finite products. It follows that it preserves group objects. Since a group object in
![]() $\mathrm{Set}^{\mathscr{S}}$
is simply an object-wise group object, we get a natural group structure on
$\mathrm{Set}^{\mathscr{S}}$
is simply an object-wise group object, we get a natural group structure on
![]() ${\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s) $
. To show that this group is the colimit of G, we need to construct a universal cocone
${\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s) $
. To show that this group is the colimit of G, we need to construct a universal cocone
![]() $ \big( G_s \to {\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s) \big)_{s : \mathscr{S}} $
in
$ \big( G_s \to {\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s) \big)_{s : \mathscr{S}} $
in
![]() $\mathscr{A}$
.
$\mathscr{A}$
.
The multiplication map on
![]() ${\mathrm{colim}_{s : S}}\, U(G_s)$
is induced from all the multiplication maps
${\mathrm{colim}_{s : S}}\, U(G_s)$
is induced from all the multiplication maps
![]() $ G_s \times G_s \to G_s$
using functoriality of the colimit and that
$ G_s \times G_s \to G_s$
using functoriality of the colimit and that
![]() ${\mathrm{colim}_{\mathscr{S}}}$
preserves binary products. Thus, the natural maps
${\mathrm{colim}_{\mathscr{S}}}$
preserves binary products. Thus, the natural maps
![]() $i_s : G_s \to {\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s)$
are group homomorphisms (not just maps), giving a cocone of the desired form. For any other cocone
$i_s : G_s \to {\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s)$
are group homomorphisms (not just maps), giving a cocone of the desired form. For any other cocone
![]() $ (f_s : G_s \to H)_{s : \mathscr{S}}$
in
$ (f_s : G_s \to H)_{s : \mathscr{S}}$
in
![]() $\mathscr{A}$
, we get an induced map
$\mathscr{A}$
, we get an induced map
![]() $f : {\mathrm{colim}_{s:\mathscr{S}}}\, U(G_s) \to UH$
of sets. Since
$f : {\mathrm{colim}_{s:\mathscr{S}}}\, U(G_s) \to UH$
of sets. Since
![]() $f_s(-) \cdot_H f_s(-) = f_s(- \cdot_{G_s} -) $
for any
$f_s(-) \cdot_H f_s(-) = f_s(- \cdot_{G_s} -) $
for any
![]() $ s : \mathscr{S}$
, uniqueness of maps out of colimits gives that
$ s : \mathscr{S}$
, uniqueness of maps out of colimits gives that
![]() $ f(-) \cdot f(-) = f(- \cdot -) $
. In other words, f is a group homomorphism. This means that the cocone
$ f(-) \cdot f(-) = f(- \cdot -) $
. In other words, f is a group homomorphism. This means that the cocone
![]() $(i_s : G_s \to {\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s))_{s : \mathscr{S}} $
is a universal cocone under G in
$(i_s : G_s \to {\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s))_{s : \mathscr{S}} $
is a universal cocone under G in
![]() $\mathscr{A}$
, as desired.
$\mathscr{A}$
, as desired.
Now we consider the case when
![]() $\mathscr{A}$
is the category of R-modules for a ring R. It is straightforward to check that colimits of R-modules may be computed on the underlying abelian groups, as in classical algebra. Thus, we need only consider the case when
$\mathscr{A}$
is the category of R-modules for a ring R. It is straightforward to check that colimits of R-modules may be computed on the underlying abelian groups, as in classical algebra. Thus, we need only consider the case when
![]() $R \equiv {\mathbb{Z}}$
. But if G is a diagram of abelian groups in the argument above, then
$R \equiv {\mathbb{Z}}$
. But if G is a diagram of abelian groups in the argument above, then
![]() ${\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s)$
is also abelian, because
${\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s)$
is also abelian, because
![]() ${\mathrm{colim}_{\mathscr{S}}} : \mathrm{Set}^{\mathscr{S}} \to \mathrm{Set}$
also preserves abelian group objects. But then we are done since
${\mathrm{colim}_{\mathscr{S}}} : \mathrm{Set}^{\mathscr{S}} \to \mathrm{Set}$
also preserves abelian group objects. But then we are done since
![]() ${\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s)$
has the required universal property.
${\mathrm{colim}_{s : \mathscr{S}}}\, U(G_s)$
has the required universal property.
2.3 Filtered colimits
Filtered colimits of sets have particularly nice descriptions, and it is well known that they commute with finite limits, classically. Less known is that fact that filtered colimits actually commute with finitely generated limits (Definition 2.3.2). We start with the relevant definitions.
Definition 2.3.1 A precategory
![]() $ \mathscr{F} $
is filtered if the following propositions all hold:
$ \mathscr{F} $
is filtered if the following propositions all hold:
-
(1)
 $ \mathscr{F} $
is merely inhabited;
$ \mathscr{F} $
is merely inhabited; -
(2) for any two objects
 $ c, c' : \mathscr{F,} $
there merely exists an upper bound
$ c, c' : \mathscr{F,} $
there merely exists an upper bound
 $ c \to c'' \leftarrow c' $
;
$ c \to c'' \leftarrow c' $
; -
(3) for any two arrows
 $ f, g : c \to c', $
there merely exists some
$ f, g : c \to c', $
there merely exists some
 $ h : c' \to c'' $
such that
$ h : c' \to c'' $
such that
 $ hf = hg $
.
$ hf = hg $
.
By definition, filteredness is a property of a precategory. It is straightforward to prove, by induction, that any finite family of objects in a filtered category merely admits an upper bound. Similarly, any finite number of parallel arrows merely admit a (not necessarily universal) coequalising arrow. Here, by ‘finite’ we mean Bishop-finite. That is, a type X for which there merely exists a natural number
![]() $n : {\mathbb{N}}$
and an equivalence
$n : {\mathbb{N}}$
and an equivalence
![]() ${\mathrm{Fin}(n)} \simeq X$
, where
${\mathrm{Fin}(n)} \simeq X$
, where
![]() ${\mathrm{Fin}(n)}$
denotes the standard n-element set.
${\mathrm{Fin}(n)}$
denotes the standard n-element set.
More generally, filtered categories admit cones under finitely generated diagrams.
Definition 2.3.2 A precategory
![]() $ \mathscr{D} $
is finitely generated if the underlying type of objects is Bishop-finite, and there exists a family of morphisms
$ \mathscr{D} $
is finitely generated if the underlying type of objects is Bishop-finite, and there exists a family of morphisms
![]() $ \Phi : \Pi_{i:I} \mathscr{D}(s_i, t_i) $
in
$ \Phi : \Pi_{i:I} \mathscr{D}(s_i, t_i) $
in
![]() $ \mathscr{D} $
indexed by a Bishop-finite set I, such that every morphism in
$ \mathscr{D} $
indexed by a Bishop-finite set I, such that every morphism in
![]() $ \mathscr{D} $
merely factors as follows:
$ \mathscr{D} $
merely factors as follows:
where
![]() $ {\mathrm{Fin}(n)} $
denotes the standard n-element set.
$ {\mathrm{Fin}(n)} $
denotes the standard n-element set.
Observe that a finitely generated precategory is automatically a strict category, since Bishop-finite types are necessarily sets.
Proposition 2.3.3 Let
![]() $ \mathscr{F} $
and
$ \mathscr{F} $
and
![]() $ \mathscr{D} $
be filtered and finitely generated categories, respectively. Any functor
$ \mathscr{D} $
be filtered and finitely generated categories, respectively. Any functor
![]() $ D : \mathscr{D} \to \mathscr{F} $
merely admits a cocone.
$ D : \mathscr{D} \to \mathscr{F} $
merely admits a cocone.
Proof. Lemma 2.13.2 of Borceux (Reference Borceux1994) readily generalises to the case when
![]() $ \mathscr{D} $
is finitely generated.
$ \mathscr{D} $
is finitely generated.
Using this proposition, we can easily show that filteredness implies siftedness:
Lemma 2.3.4 Filtered precategories are sifted.
Proof. Suppose
![]() $\mathscr{F}$
is a filtered precategory. To see that
$\mathscr{F}$
is a filtered precategory. To see that
![]() $\mathscr{F}$
is sifted, we need to show that the slice precategory
$\mathscr{F}$
is sifted, we need to show that the slice precategory
![]() $(c_0, c_1) / \Delta_{\mathscr{F}}$
is connected for any
$(c_0, c_1) / \Delta_{\mathscr{F}}$
is connected for any
![]() $c_0, c_1 : \mathscr{F}$
. An object of this slice is precisely an upper bound
$c_0, c_1 : \mathscr{F}$
. An object of this slice is precisely an upper bound
![]() $c_0 \to c \leftarrow c_1 $
, so the slice is merely inhabited since
$c_0 \to c \leftarrow c_1 $
, so the slice is merely inhabited since
![]() $\mathscr{F}$
is filtered. To see that the slice is connected, let c and c’ be upper bounds of
$\mathscr{F}$
is filtered. To see that the slice is connected, let c and c’ be upper bounds of
![]() $c_0$
and
$c_0$
and
![]() $c_1$
. We may form the following diagram:
$c_1$
. We may form the following diagram:

A cocone of this diagram merely exists, by the previous proposition. This cocone exhibits a zig-zag of length one connecting c and c’.
Theorem 2.3.5 Let
![]() $ \mathscr{F} $
and
$ \mathscr{F} $
and
![]() $ \mathscr{D} $
be filtered and finitely generated categories, respectively, and consider a functor
$ \mathscr{D} $
be filtered and finitely generated categories, respectively, and consider a functor
![]() $ D : \mathscr{F} \times \mathscr{D} \to \mathrm{Set} $
. The natural map
$ D : \mathscr{F} \times \mathscr{D} \to \mathrm{Set} $
. The natural map
![]() $ {\mathrm{colim}_{\mathscr{F}}}\, {\mathrm{lim}_{\mathscr{D}}}\, D \to {\mathrm{lim}_{\mathscr{D}}} {\mathrm{colim}_{\mathscr{F}}} D $
is a bijection.
$ {\mathrm{colim}_{\mathscr{F}}}\, {\mathrm{lim}_{\mathscr{D}}}\, D \to {\mathrm{lim}_{\mathscr{D}}} {\mathrm{colim}_{\mathscr{F}}} D $
is a bijection.
Proof. For finite categories
![]() $ \mathscr{D,} $
the proof of Borceux (Reference Borceux1994, Theorem 2.13.4) goes through since every application of the axiom of choice is used for a finite indexing set, which is valid in HoTT (see, e.g., Spaces.Finite.finite_choice). The generalisation to
$ \mathscr{D,} $
the proof of Borceux (Reference Borceux1994, Theorem 2.13.4) goes through since every application of the axiom of choice is used for a finite indexing set, which is valid in HoTT (see, e.g., Spaces.Finite.finite_choice). The generalisation to
![]() $ \mathscr{D} $
being finitely generated only requires straightforward modifications using Proposition 2.3.3 in the last part of Borceux’s argument.
$ \mathscr{D} $
being finitely generated only requires straightforward modifications using Proposition 2.3.3 in the last part of Borceux’s argument.
Remark 2.3.6 That filtered colimits commute with finite limits has been formalised in mathlib Community (2020) in the file category_theory/limits/filtered_colimit_commutes_finite.lean. Their proof follows that of Theorem 2.13.4 in Borceux (Reference Borceux1994), as we did; however, they freely employ classical reasoning (as Borceux does) in their formalisation. In particular, they begin their proofs by assuming the law of the excluded middle (using the classical tactic) and employ the full axiom of choice (using some to choose elements of merely inhabited sets) in the same places as Borceux. (In fact, in more places than Borceux, if you read his proof constructively.) Our contribution is simply the observation that, with our constructive definitions of limits and colimits of sets, the proof does not require the law of the excluded middle and each application of the axiom of choice is in fact an application of finite choice, which is valid for us.
We say that a group G is finitely generated if there exist a Bishop-finite generating set. Recall that a G-set X is simply a map
![]() $X : BG \to \mathrm{Set} $
(see Bezem et al. Reference Bezem, Buchholtz, Cagne, Dundas and Grayson2023, Section 4.7), and the fixed points of X are given by
$X : BG \to \mathrm{Set} $
(see Bezem et al. Reference Bezem, Buchholtz, Cagne, Dundas and Grayson2023, Section 4.7), and the fixed points of X are given by
![]() $ \Pi_{BG} X $
. As an application of our development thus far, we have the following:
$ \Pi_{BG} X $
. As an application of our development thus far, we have the following:
Corollary 2.3.7 Let G be a finitely generated group, and let
![]() $ X : \mathscr{F} \to (BG \to \mathrm{Set}) $
be a filtered diagram of G-sets. The fixed points of the colimit are the colimit of the fixed points:
$ X : \mathscr{F} \to (BG \to \mathrm{Set}) $
be a filtered diagram of G-sets. The fixed points of the colimit are the colimit of the fixed points:
Proof. The category BG is the Rezk completion of the strict category B’G which has a single object with G as its endomorphisms. If G is a finitely generated group, then B’G is a finitely generated category in the sense of Definition 2.3.2. By Proposition 2.1.6, we have that
![]() $ \Pi_{BG}(-) = {\mathrm{lim}_{BG}} (-) $
, and by Lemma 2.1.3 we can change the limits to be over B’G. Since B’G is finitely generated and
$ \Pi_{BG}(-) = {\mathrm{lim}_{BG}} (-) $
, and by Lemma 2.1.3 we can change the limits to be over B’G. Since B’G is finitely generated and
![]() $ \mathscr{F} $
is filtered, we are done by the previous theorem.
$ \mathscr{F} $
is filtered, we are done by the previous theorem.
3 The Internal AB Axioms
The goal of this section is to show that for a ring R in HoTT, the category of R-modules satisfies the axioms AB3 through AB5 and has a generator – meaning it is a Grothendieck category (Definition 3.1.3). Formally, a Grothendieck category is only assumed to satisfy AB3 and AB5, but we show that AB4 follows from AB5 (Theorem 3.3.10). It is straightforward to check that
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
is an abelian category in HoTT, and indeed this has already been formalised for
$ {{R}\textrm{-}{\mathrm{Mod}}} $
is an abelian category in HoTT, and indeed this has already been formalised for
![]() $ R \equiv {\mathbb{Z}} $
in the file CategoryTheory/categories/abgrs.v of the Voevodsky et al. (https://unimath.org) library. (Some work towards the general case can be found in the file modules.v in the same directory.) Moreover, R being a generator is simply a restatement of function extensionality. What remains is to show that
$ R \equiv {\mathbb{Z}} $
in the file CategoryTheory/categories/abgrs.v of the Voevodsky et al. (https://unimath.org) library. (Some work towards the general case can be found in the file modules.v in the same directory.) Moreover, R being a generator is simply a restatement of function extensionality. What remains is to show that
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
satisfies the axioms AB3 through AB5.
$ {{R}\textrm{-}{\mathrm{Mod}}} $
satisfies the axioms AB3 through AB5.
We wish to treat families
![]() $ A : X \to \mathscr{A} $
in an abelian category
$ A : X \to \mathscr{A} $
in an abelian category
![]() $ \mathscr{A} $
indexed by an arbitrary type X. As pointed out at the beginning of Section 2, we think of these as functors from an
$ \mathscr{A} $
indexed by an arbitrary type X. As pointed out at the beginning of Section 2, we think of these as functors from an
![]() $ \infty $
-groupoid into a category. Since
$ \infty $
-groupoid into a category. Since
![]() $ \mathscr{A} $
is a category, its underlying type is 1-truncated, and so we may factor any such family A through the 1-truncation of X. One checks that the 1-truncation map
$ \mathscr{A} $
is a category, its underlying type is 1-truncated, and so we may factor any such family A through the 1-truncation of X. One checks that the 1-truncation map
![]() $ {\lvert - \lvert }_1 : X \to {\lVert X \lVert }_1 $
induces an equivalence of categories by precomposition:
$ {\lvert - \lvert }_1 : X \to {\lVert X \lVert }_1 $
induces an equivalence of categories by precomposition:
It follows, by an argument similar to the one in Lemma 2.1.3, that the limit (resp. colimit) of a functor
![]() $ A : X \to \mathscr{A} $
coincides with the limit (resp. colimit) of the 1-truncation
$ A : X \to \mathscr{A} $
coincides with the limit (resp. colimit) of the 1-truncation
![]() $ {\lvert A \lvert }_1 : {\lVert X \lVert }_1 \to \mathscr{A} $
. (Limits and colimits of functors from an
$ {\lvert A \lvert }_1 : {\lVert X \lVert }_1 \to \mathscr{A} $
. (Limits and colimits of functors from an
![]() $ \infty $
-groupoid into a category are defined in the obvious way.) Thus, when we discuss limits and colimits of such a family A, we may assume that X is a 1-type without loss of generality.
$ \infty $
-groupoid into a category are defined in the obvious way.) Thus, when we discuss limits and colimits of such a family A, we may assume that X is a 1-type without loss of generality.
3.1 Grothendieck categories
We define Grothendieck abelian categories in HoTT, assuming the reader is familiar with additive and abelian precategories. The traditional definitions of the latter can be directly translated into our setting, as has already been done in Voevodsky et al. (https://unimath.org) under the namespace CategoryTheory/Abelian. Be aware that by abelian category we do mean that it is a (univalent) category. While much of our discussion likely works for abelian precategories as well, we are particularly interested in discussing families of objects and their (co)limits, which is most naturally done for categories.
Definition 3.1.1 Let
![]() $ \mathscr{A} $
be an additive category, and X a set. For a family
$ \mathscr{A} $
be an additive category, and X a set. For a family
![]() $ A : X \to \mathscr{A} $
, the coproduct of A (if it exists) is the colimit of A, denoted
$ A : X \to \mathscr{A} $
, the coproduct of A (if it exists) is the colimit of A, denoted
![]() $ \bigoplus_{x:X} A(x) $
. Dually, the product of A (if it exists) is the limit of A, denoted
$ \bigoplus_{x:X} A(x) $
. Dually, the product of A (if it exists) is the limit of A, denoted
![]() $ \Pi_{x:X} A(x) $
. If no confusion will arise, we often leave the variable
$ \Pi_{x:X} A(x) $
. If no confusion will arise, we often leave the variable
![]() $ x : X$
implicit.
$ x : X$
implicit.
Suppose
![]() $ \mathscr{A} $
is an additive category. Then, by definition, finite products and coproducts in
$ \mathscr{A} $
is an additive category. Then, by definition, finite products and coproducts in
![]() $ \mathscr{A} $
coincide, and we call these biproducts. The word finite here means ‘finitely iterated’, meaning pairwise biproducts carried out a finite number of times. If X is a decidable set, and
$ \mathscr{A} $
coincide, and we call these biproducts. The word finite here means ‘finitely iterated’, meaning pairwise biproducts carried out a finite number of times. If X is a decidable set, and
![]() $ A : X \to \mathscr{A} $
is a family, then there is always a comparison map
$ A : X \to \mathscr{A} $
is a family, then there is always a comparison map
![]() $ m : \bigoplus_X A \to \Pi_X A $
which is a monomorphism. This is straightforward to prove in HoTT (and was shown for families of modules in an elementary topos with
$ m : \bigoplus_X A \to \Pi_X A $
which is a monomorphism. This is straightforward to prove in HoTT (and was shown for families of modules in an elementary topos with
![]() $ {\mathbb{N}} $
in Tavakoli Reference Tavakoli1985) Of course, if X is the standard n-element set
$ {\mathbb{N}} $
in Tavakoli Reference Tavakoli1985) Of course, if X is the standard n-element set
![]() $ {\mathrm{Fin}(n)} $
for some
$ {\mathrm{Fin}(n)} $
for some
![]() $ n : {\mathbb{N}} $
, then the map m is an isomorphism. We deduce the following, since m being an isomorphism is a proposition:
$ n : {\mathbb{N}} $
, then the map m is an isomorphism. We deduce the following, since m being an isomorphism is a proposition:
Lemma 3.1.2 Let
![]() $ \mathscr{A} $
be an additive category, and X a Bishop-finite type. For any family
$ \mathscr{A} $
be an additive category, and X a Bishop-finite type. For any family
![]() $ A : X \to \mathscr{A} $
, the natural map
$ A : X \to \mathscr{A} $
, the natural map
![]() $ m : \bigoplus_X A \to \Pi_X A $
is an isomorphism.
$ m : \bigoplus_X A \to \Pi_X A $
is an isomorphism.
It may come as a surprise that no such monomorphism m need exist in general. In fact, Harting demonstrates in (1982, Remark 2.1) that there might be no non-trivial map like m. Her example is in the Sierpi
![]() ${\rm n'}$
ski 1-topos, which is the 0-truncated fragment of the Sierpi
${\rm n'}$
ski 1-topos, which is the 0-truncated fragment of the Sierpi
![]() ${\rm n'}$
ski
${\rm n'}$
ski
![]() $\infty$
-topos (see Proposition 4.2.4). The latter is a model of HoTT, and Harting’s example therefore shows that it is impossible for us to construct a non-zero map
$\infty$
-topos (see Proposition 4.2.4). The latter is a model of HoTT, and Harting’s example therefore shows that it is impossible for us to construct a non-zero map
![]() $ \bigoplus_X A \to \Pi_X A $
for a general set X. The example also demonstrates that the construction of arbitrary coproducts is tricky; for example, one cannot carve out
$ \bigoplus_X A \to \Pi_X A $
for a general set X. The example also demonstrates that the construction of arbitrary coproducts is tricky; for example, one cannot carve out
![]() $ \bigoplus_X A $
from
$ \bigoplus_X A $
from
![]() $ \Pi_X A$
as those families with ‘finite support’. We will have more to say about models of HoTT in Section 4 below. For more details about the Sierpi
$ \Pi_X A$
as those families with ‘finite support’. We will have more to say about models of HoTT in Section 4 below. For more details about the Sierpi
![]() ${\rm n'}$
ski
${\rm n'}$
ski
![]() $\infty$
-topos specifically, we recommend (2015, Section 8).
$\infty$
-topos specifically, we recommend (2015, Section 8).
Definition 3.1.3 For an abelian category
![]() $ \mathscr{A,} $
we consider the following axioms.
$ \mathscr{A,} $
we consider the following axioms.
(AB3) for any small set X and family
![]() $ A : X \to \mathscr{A} $
, the coproduct
$ A : X \to \mathscr{A} $
, the coproduct
![]() $ \bigoplus_X A $
exists in
$ \bigoplus_X A $
exists in
![]() $ \mathscr{A} $
;
$ \mathscr{A} $
;
Assuming
![]() $ \mathscr{A} $
satisfies AB3, we get a coproduct functor
$ \mathscr{A} $
satisfies AB3, we get a coproduct functor
![]() $ \bigoplus_X : \mathscr{A}^X \to \mathscr{A}$
. It also follows that
$ \bigoplus_X : \mathscr{A}^X \to \mathscr{A}$
. It also follows that
![]() $\mathscr{A}$
is cocomplete (since it always has coequalisers). Thus, assuming AB3, we may additionally ask for:
$\mathscr{A}$
is cocomplete (since it always has coequalisers). Thus, assuming AB3, we may additionally ask for:
(AB4) for any small set X, the functor
![]() $\bigoplus_X : \mathscr{A}^X \to \mathscr{A}$
preserves monomorphisms;
$\bigoplus_X : \mathscr{A}^X \to \mathscr{A}$
preserves monomorphisms;
(AB5) for any small filtered precategory
![]() $ \mathscr{F} $
, the functor
$ \mathscr{F} $
, the functor
![]() $ {\mathrm{colim}_{\mathscr{F}}} : \mathscr{A}^\mathscr{F} \to \mathscr{A} $
preserves finite limits.
$ {\mathrm{colim}_{\mathscr{F}}} : \mathscr{A}^\mathscr{F} \to \mathscr{A} $
preserves finite limits.
A generator of
![]() $ \mathscr{A} $
is an object
$ \mathscr{A} $
is an object
![]() $ G : \mathscr{A} $
such that for any two morphisms
$ G : \mathscr{A} $
such that for any two morphisms
![]() $ f, f' : A \to B $
, we have
$ f, f' : A \to B $
, we have
When
![]() $\mathscr{A}$
has a specified generator and satisfies AB3 and AB5, then
$\mathscr{A}$
has a specified generator and satisfies AB3 and AB5, then
![]() $\mathscr{A}$
is a Grothendieck category.
$\mathscr{A}$
is a Grothendieck category.
We note that monomorphisms in
![]() $\mathscr{A}^X$
are object-wise monomorphisms (i.e., families of such). The axiom AB5 implies that the colimit functor
$\mathscr{A}^X$
are object-wise monomorphisms (i.e., families of such). The axiom AB5 implies that the colimit functor
![]() $ {\mathrm{colim}_{\mathscr{F}}} $
is exact for filtered precategories
$ {\mathrm{colim}_{\mathscr{F}}} $
is exact for filtered precategories
![]() $ \mathscr{F} $
. In the next section, we show that
$ \mathscr{F} $
. In the next section, we show that
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
is Grothendieck for any ring R.
$ {{R}\textrm{-}{\mathrm{Mod}}} $
is Grothendieck for any ring R.
3.2 Colimits of R-modules
We consider a 1-type X as a category and construct an adjunction:
When X is a set, the colimit is the coproduct of an X-indexed family of modules. In contrast, when
![]() $ R \equiv {\mathbb{Z}} $
and X is pointed and connected,
$ R \equiv {\mathbb{Z}} $
and X is pointed and connected,
![]() $ {{R}\textrm{-}{\mathrm{Mod}}}^X $
is the category of
$ {{R}\textrm{-}{\mathrm{Mod}}}^X $
is the category of
![]() $ \pi_1(X) $
-modules (Definition 3.2.4). We will see that the functor
$ \pi_1(X) $
-modules (Definition 3.2.4). We will see that the functor
![]() $ {\mathrm{colim}_{X}} $
computes the coinvariants of a
$ {\mathrm{colim}_{X}} $
computes the coinvariants of a
![]() $ \pi_1(X) $
-module. Dually, the functor
$ \pi_1(X) $
-module. Dually, the functor
![]() $ {\mathrm{lim}_{X}} $
computes the invariants.
$ {\mathrm{lim}_{X}} $
computes the invariants.
As in classical algebra, the forgetful functor
![]() $ U : {{R}\textrm{-}{\mathrm{Mod}}} \to {\mathrm{Ab}} $
creates limits and colimits. Thus, by constructing
$ U : {{R}\textrm{-}{\mathrm{Mod}}} \to {\mathrm{Ab}} $
creates limits and colimits. Thus, by constructing
![]() $ {\mathrm{colim}_{X}} $
for families of abelian groups, we extend it to families of modules via U. Moreover, the category of abelian groups is equivalent to the category of pointed, 1-connected 2-types (Buchholtz et al., Reference Buchholtz, van Doorn and Rijke2018, Theorem 5.1) through the functor
$ {\mathrm{colim}_{X}} $
for families of abelian groups, we extend it to families of modules via U. Moreover, the category of abelian groups is equivalent to the category of pointed, 1-connected 2-types (Buchholtz et al., Reference Buchholtz, van Doorn and Rijke2018, Theorem 5.1) through the functor
![]() ${\mathrm{K}({-},{2})}$
(whose inverse is
${\mathrm{K}({-},{2})}$
(whose inverse is
![]() $\Omega^2$
). The latter category is cocomplete, so we can transfer colimits across this equivalence. We now give an explicit account of this procedure.
$\Omega^2$
). The latter category is cocomplete, so we can transfer colimits across this equivalence. We now give an explicit account of this procedure.
Proposition 3.2.1 Let X be a 1-type. We have an adjunction
![]() $ {\mathrm{colim}_{X}} : {\mathrm{Ab}}^X \leftrightarrows {\mathrm{Ab}} : {\mathrm{const}_{X}} $
.
$ {\mathrm{colim}_{X}} : {\mathrm{Ab}}^X \leftrightarrows {\mathrm{Ab}} : {\mathrm{const}_{X}} $
.
Proof. We start by constructing the functor
![]() $ {\mathrm{colim}_{X}} $
. Let
$ {\mathrm{colim}_{X}} $
. Let
![]() $ A : X \to {\mathrm{Ab}} $
. Via Buchholtz et al. (Reference Buchholtz, van Doorn and Rijke2018, Theorem 5.1), we may instead consider the corresponding family
$ A : X \to {\mathrm{Ab}} $
. Via Buchholtz et al. (Reference Buchholtz, van Doorn and Rijke2018, Theorem 5.1), we may instead consider the corresponding family
![]() $ x \mapsto {\mathrm{K}({A(x)},{2})}$
of pointed, 1-connected 2-types. The colimit of this family among types is then
$ x \mapsto {\mathrm{K}({A(x)},{2})}$
of pointed, 1-connected 2-types. The colimit of this family among types is then
![]() $ \Sigma_{X} {\mathrm{K}({A},{2})} $
by Lemma 2.1.5, whereas the colimit among pointed types is the pushout
$ \Sigma_{X} {\mathrm{K}({A},{2})} $
by Lemma 2.1.5, whereas the colimit among pointed types is the pushout

called the indexed wedge. Thus the colimit of
![]() ${\mathrm{K}({A},{2})}$
among pointed 2-types is
${\mathrm{K}({A},{2})}$
among pointed 2-types is
![]() ${\lVert { \bigvee_{X} {\mathrm{K}({A},{2})} }\lVert }_2$
by The Univalent Foundations Program (2013, Section 7.4). Moreover, by Theorem 7.3.9 in The Univalent Foundations Program (2013) we have that
${\lVert { \bigvee_{X} {\mathrm{K}({A},{2})} }\lVert }_2$
by The Univalent Foundations Program (2013, Section 7.4). Moreover, by Theorem 7.3.9 in The Univalent Foundations Program (2013) we have that
using that
![]() $ {{\mathrm{K}({A(x)},{2})}} $
is 1-connected for all
$ {{\mathrm{K}({A(x)},{2})}} $
is 1-connected for all
![]() $ x : X $
, and that X is a 1-type. From this, we deduce that 1-truncating the pushout square above produces
$ x : X $
, and that X is a 1-type. From this, we deduce that 1-truncating the pushout square above produces

since pushouts commute with truncation. In particular,
![]() $ \bigvee_X {{\mathrm{K}({A},{2})}}$
is 1-connected. Finally, since
$ \bigvee_X {{\mathrm{K}({A},{2})}}$
is 1-connected. Finally, since
![]() $ {\lVert { \bigvee_{X} {{\mathrm{K}({A},{2})}} }\lVert }_2 $
has the desired universal property among pointed 2-types, it certainly has it among pointed, 1-connected 2-types, being one itself. Now we apply
$ {\lVert { \bigvee_{X} {{\mathrm{K}({A},{2})}} }\lVert }_2 $
has the desired universal property among pointed 2-types, it certainly has it among pointed, 1-connected 2-types, being one itself. Now we apply
![]() $ \Omega^2 $
, the inverse of
$ \Omega^2 $
, the inverse of
![]() $ {{\mathrm{K}({-},{2})}} $
, and move the truncation to the outermost level, to define our functor on objects:
$ {{\mathrm{K}({-},{2})}} $
, and move the truncation to the outermost level, to define our functor on objects:
 \[ {\mathrm{colim}_{X}}(A) := \pi_2 \left ( \bigvee_{X} {{\mathrm{K}({A},{2})}} \right ) . \]
\[ {\mathrm{colim}_{X}}(A) := \pi_2 \left ( \bigvee_{X} {{\mathrm{K}({A},{2})}} \right ) . \]
As defined,
![]() $ {\mathrm{colim}_{X}} $
is a composite of the functors; hence, it is itself a functor.
$ {\mathrm{colim}_{X}} $
is a composite of the functors; hence, it is itself a functor.
Corollary 3.2.2 Let R be a ring. The category
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
is complete and cocomplete.
$ {{R}\textrm{-}{\mathrm{Mod}}} $
is complete and cocomplete.
Proof. We reduce to
![]() $ R \equiv {\mathbb{Z}} $
since the forgetful functor creates both limits and colimits. For limits, note that
$ R \equiv {\mathbb{Z}} $
since the forgetful functor creates both limits and colimits. For limits, note that
![]() $ {\mathrm{Ab}} $
has small products given simply by the
$ {\mathrm{Ab}} $
has small products given simply by the
![]() $ \Pi $
-type of a family
$ \Pi $
-type of a family
![]() $ X \to {\mathrm{Ab}} $
indexed by a set. Since
$ X \to {\mathrm{Ab}} $
indexed by a set. Since
![]() $ {\mathrm{Ab}} $
has equalisers, it is complete. Dually, Proposition 3.2.1 produces small coproducts by letting X be a set. Since
$ {\mathrm{Ab}} $
has equalisers, it is complete. Dually, Proposition 3.2.1 produces small coproducts by letting X be a set. Since
![]() $ {\mathrm{Ab}} $
has coequalisers, it is cocomplete.
$ {\mathrm{Ab}} $
has coequalisers, it is cocomplete.
Theorem 3.2.3 The category
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
is Grothendieck.
$ {{R}\textrm{-}{\mathrm{Mod}}} $
is Grothendieck.
Proof. That R is a generator is an immediate consequence of function extensionality. By the previous corollary,
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
is cocomplete and therefore satisfies AB3. The axiom AB5 follows from Theorem 2.3.5, since products of modules are computed on the underlying sets, and the forgetful functor
$ {{R}\textrm{-}{\mathrm{Mod}}} $
is cocomplete and therefore satisfies AB3. The axiom AB5 follows from Theorem 2.3.5, since products of modules are computed on the underlying sets, and the forgetful functor
![]() ${{R}\textrm{-}{\mathrm{Mod}}}\to \mathrm{Set}$
creates sifted (hence filtered) colimits by Corollary 2.2.6.
${{R}\textrm{-}{\mathrm{Mod}}}\to \mathrm{Set}$
creates sifted (hence filtered) colimits by Corollary 2.2.6.
At this point, it is not obvious that
![]() $ {{R}\textrm{-}{\mathrm{Mod}}} $
satisfies AB4. This will be a consequence of Theorem 3.3.10 in the next section. For the remainder of this section, we discuss
$ {{R}\textrm{-}{\mathrm{Mod}}} $
satisfies AB4. This will be a consequence of Theorem 3.3.10 in the next section. For the remainder of this section, we discuss
![]() $ {\mathrm{colim}_{X}} $
when X is the classifying space of a group.
$ {\mathrm{colim}_{X}} $
when X is the classifying space of a group.
Definition 3.2.4 Let G be a group. A family
![]() $ A : BG \to {\mathrm{Ab}} $
is a G -module. The invariants of A comprise the abelian group
$ A : BG \to {\mathrm{Ab}} $
is a G -module. The invariants of A comprise the abelian group
![]() $ A_G := {\mathrm{lim}_{BG}}\, A $
, and the coinvariants comprise the abelian group
$ A_G := {\mathrm{lim}_{BG}}\, A $
, and the coinvariants comprise the abelian group
![]() $ A^G := {\mathrm{colim}_{BG}}\, A $
.
$ A^G := {\mathrm{colim}_{BG}}\, A $
.
Using the fact that limits of abelian groups may be computed on the underlying sets, along with the concrete description of limits in Proposition 2.1.4, we see that
![]() $ A_G = \{ a : A \mid \Pi_{g: G} \ ga = a \} $
, which is the usual definition of the invariants. Writing
$ A_G = \{ a : A \mid \Pi_{g: G} \ ga = a \} $
, which is the usual definition of the invariants. Writing
![]() $ {\mathrm{colim}_{BG}}\, A $
as a coequaliser produces
$ {\mathrm{colim}_{BG}}\, A $
as a coequaliser produces

from which we see that
![]() $ A^G $
is the quotient of A by the subgroup
$ A^G $
is the quotient of A by the subgroup
![]() $ \langle a - ga \mid g : G \rangle $
, which is the usual definition of the coinvariants.
$ \langle a - ga \mid g : G \rangle $
, which is the usual definition of the coinvariants.
We now relate some of Harting’s considerations about coproducts to our colimits, which are their higher analogues. To that end, we consider the group
![]() $G := {\mathbb{Z}} / 2$
in the remark and example below. A G -module is then an abelian group equipped with an automorphism which squares to the identity.
$G := {\mathbb{Z}} / 2$
in the remark and example below. A G -module is then an abelian group equipped with an automorphism which squares to the identity.
Remark 3.2.5 After Definition 3.1.1, we discussed Harting’s counterexample to the existence of a monomorphism
![]() $ \bigoplus_X A \to \Pi_X A $
when X is a set. Of course, this also means that there is in general no monomorphism
$ \bigoplus_X A \to \Pi_X A $
when X is a set. Of course, this also means that there is in general no monomorphism
![]() $ {\mathrm{colim}_{X}}\, A \to {\mathrm{lim}_{X}}\, A $
when X is not necessarily a set, but it is much easier to produce a counterexample to this. For example, if we consider the G-module
$ {\mathrm{colim}_{X}}\, A \to {\mathrm{lim}_{X}}\, A $
when X is not necessarily a set, but it is much easier to produce a counterexample to this. For example, if we consider the G-module
![]() $ {\mathbb{Z}} $
given by the negation automorphism
$ {\mathbb{Z}} $
given by the negation automorphism
![]() $n \mapsto -n$
, then the coinvariants are
$n \mapsto -n$
, then the coinvariants are
![]() $ {\mathbb{Z}}^G = {\mathbb{Z}} / 2 $
but the invariants are
$ {\mathbb{Z}}^G = {\mathbb{Z}} / 2 $
but the invariants are
![]() $ {\mathbb{Z}}_G = 0 $
. Of course, there are no monomorphisms
$ {\mathbb{Z}}_G = 0 $
. Of course, there are no monomorphisms
![]() ${\mathbb{Z}} / 2 \to 0$
.
${\mathbb{Z}} / 2 \to 0$
.
In Harting (Reference Harting1982), Harting carried out her specific construction of the internal coproduct of abelian groups so as to prove that the resulting coproduct functor was left-exact (in particular, it preserves monomorphisms). For us, the internal coproduct is
![]() $ {\mathrm{colim}_{X}} $
for a set X. Here, we demonstrate that
$ {\mathrm{colim}_{X}} $
for a set X. Here, we demonstrate that
![]() $ {\mathrm{colim}_{X}} $
generally fails to be left-exact when X is not a set.
$ {\mathrm{colim}_{X}} $
generally fails to be left-exact when X is not a set.
Example 3.2.6 Consider the G -module
![]() $ {\mathbb{Z}} $
equipped with the negation automorphism
$ {\mathbb{Z}} $
equipped with the negation automorphism
![]() $ n \mapsto -n $
, and the G -module
$ n \mapsto -n $
, and the G -module
![]() $ {\mathbb{Z}} \times {\mathbb{Z}} $
equipped with the ‘swap’ automorphism
$ {\mathbb{Z}} \times {\mathbb{Z}} $
equipped with the ‘swap’ automorphism
![]() $ (a,b) \mapsto (b,a) $
. We have a G-equivariant monomorphism
$ (a,b) \mapsto (b,a) $
. We have a G-equivariant monomorphism
![]() $ 1 \mapsto (-1, 1) : {\mathbb{Z}} \to {\mathbb{Z}} \times {\mathbb{Z}} $
which fails to induce a monomorphism on the coinvariants. Explicitly, the respective coinvariants are
$ 1 \mapsto (-1, 1) : {\mathbb{Z}} \to {\mathbb{Z}} \times {\mathbb{Z}} $
which fails to induce a monomorphism on the coinvariants. Explicitly, the respective coinvariants are
![]() $ {\mathbb{Z}}^G = {\mathbb{Z}} / 2 $
and
$ {\mathbb{Z}}^G = {\mathbb{Z}} / 2 $
and
![]() $ ({\mathbb{Z}} \times {\mathbb{Z}})^G = {\mathbb{Z}} $
. There are of course no non-trivial homomorphisms
$ ({\mathbb{Z}} \times {\mathbb{Z}})^G = {\mathbb{Z}} $
. There are of course no non-trivial homomorphisms
![]() $ {\mathbb{Z}}/2 \to {\mathbb{Z}} $
, and certainly no monomorphisms. Consequently, the functor
$ {\mathbb{Z}}/2 \to {\mathbb{Z}} $
, and certainly no monomorphisms. Consequently, the functor
![]() $ {\mathrm{colim}_{B ({\mathbb{Z}} / 2)}} $
, which computes the coinvariants, is not left-exact.
$ {\mathrm{colim}_{B ({\mathbb{Z}} / 2)}} $
, which computes the coinvariants, is not left-exact.
3.3 AB5 implies AB4
We prove that AB4 follows from AB5 for any abelian category, as is familiar in ordinary homological algebra. The classical proof proceeds by replacing a discrete indexing category X (for a coproduct) by a filtered category (the finite subsets of X) sharing the same colimit, then applying AB5. However, in a constructive setting neither the category of Bishop-finite subsets of X nor the category of ordered finite subsets of X is filtered unless X is decidable. For this reason, we will work with lists of elements in X, meaning general maps of the form
![]() $ {\mathrm{Fin}(n)} \to X $
as opposed to only the injections.
$ {\mathrm{Fin}(n)} \to X $
as opposed to only the injections.
We wish to point out that this is how Harting constructs the internal coproduct of abelian groups in an elementary topos (with
![]() $ {\mathbb{N}} $
) in Harting (Reference Harting1982), though she does not phrase things in terms of the AB axioms. While the goal of this construction is to realise a coproduct as a filtered colimit, we find it interesting to observe that Harting’s ‘set-theoretic’ description readily generalises to untruncated indexing types, as well as abelian categories
$ {\mathbb{N}} $
) in Harting (Reference Harting1982), though she does not phrase things in terms of the AB axioms. While the goal of this construction is to realise a coproduct as a filtered colimit, we find it interesting to observe that Harting’s ‘set-theoretic’ description readily generalises to untruncated indexing types, as well as abelian categories
![]() $ \mathscr{A} $
. Specifically, given a family
$ \mathscr{A} $
. Specifically, given a family
![]() $ A : X \to \mathscr{A} $
indexed by an arbitrary type X, we replace A by a sifted diagram
$ A : X \to \mathscr{A} $
indexed by an arbitrary type X, we replace A by a sifted diagram
![]() $ GA : HX \to \mathscr{A} $
sharing the same colimit (if it exists). If X is a set, so the colimit is the coproduct, then
$ GA : HX \to \mathscr{A} $
sharing the same colimit (if it exists). If X is a set, so the colimit is the coproduct, then
![]() $ \bigoplus_{x:X} A(x) $
will be a filtered colimit, as desired.
$ \bigoplus_{x:X} A(x) $
will be a filtered colimit, as desired.
Our first objective is to define the precategory HX of lists of elements in any 1-type X. In general, HX will be sifted and even filtered when X is a set. The latter situation is essentially the one studied in Johnstone and Wraith (Reference Johnstone and Wraith1978, pp. 177–178). Throughout this section, let X be a 1-type (unless otherwise stated), and let
![]() $ \mathscr{A} $
be an abelian category. We implicitly identify
$ \mathscr{A} $
be an abelian category. We implicitly identify
![]() $ X^n $
and
$ X^n $
and
![]() $ {\mathrm{Fin}(n)} \to X $
where
$ {\mathrm{Fin}(n)} \to X $
where
![]() $ {\mathrm{Fin}(n)} $
is the standard n-element set.
$ {\mathrm{Fin}(n)} $
is the standard n-element set.
Definition 3.3.1 The 1-type
![]() $ HX := \Sigma_{n: {\mathbb{N}}} X^n $
becomes a precategory as follows. Given two elements
$ HX := \Sigma_{n: {\mathbb{N}}} X^n $
becomes a precategory as follows. Given two elements
![]() $ (n,x) , (m,y) : \Sigma_{n : {\mathbb{N}}} X^n $
, a morphism is a commuting triangle (with specified witness of commutativity):
$ (n,x) , (m,y) : \Sigma_{n : {\mathbb{N}}} X^n $
, a morphism is a commuting triangle (with specified witness of commutativity):
Since X is a 1-type, so is
![]() $ X^n $
, and this hom-type is therefore a set, as required for being a precategory. Identity morphisms are given by identity maps and reflexivity paths. Composing morphisms is done by pasting triangles. Specifically, if
$ X^n $
, and this hom-type is therefore a set, as required for being a precategory. Identity morphisms are given by identity maps and reflexivity paths. Composing morphisms is done by pasting triangles. Specifically, if
![]() $(f,p) : (n,x) \to (m,y)$
and
$(f,p) : (n,x) \to (m,y)$
and
![]() $(g,q) : (m,y) \to (l,z) $
are two morphisms in HX, then their composite is
$(g,q) : (m,y) \to (l,z) $
are two morphisms in HX, then their composite is
where we view q as a homotopy
![]() $ \Pi_{i : {\mathrm{Fin}(m)}} y_i = z_{g(i)} $
via function extensionality. Associativity of composition follows from associativity of function composition and path composition. Clearly, the identity maps form left- and right-units for the composition operation, meaning we have defined a precategory structure on HX.
$ \Pi_{i : {\mathrm{Fin}(m)}} y_i = z_{g(i)} $
via function extensionality. Associativity of composition follows from associativity of function composition and path composition. Clearly, the identity maps form left- and right-units for the composition operation, meaning we have defined a precategory structure on HX.
We observe the following lemma (using Lemma 2.2.4), which in general fails for the precategories of Bishop-finite or finite ordered subsets of X.
Lemma 3.3.2 The precategory HX has binary coproducts. In particular, it is sifted.
The next proposition is Johnstone and Wraith (Reference Johnstone and Wraith1978, Lemma 4.4) translated to our setting. (The precise relation being that a presheaf is flat if and only if its category of elements or ‘total category’ is filtered; see also Johnstone and Wraith Reference Johnstone and Wraith1978, Proposition 1.3.) Note that
![]() $ \Sigma_{n : {\mathbb{N}}} X^n $
is a set if X is, and HX is then a strict category. In this situation, when discussing morphisms in HX we may omit references to the commutativity witnesses.
$ \Sigma_{n : {\mathbb{N}}} X^n $
is a set if X is, and HX is then a strict category. In this situation, when discussing morphisms in HX we may omit references to the commutativity witnesses.
Proposition 3.3.3 If X is a set, then HX is filtered.
Proof. Clearly HX is merely inhabited, and coproducts yield upper bounds. It remains to verify that for any two parallel arrows
![]() $f, g : (n,x) \to (m,y)$
in HX, there merely exists an arrow
$f, g : (n,x) \to (m,y)$
in HX, there merely exists an arrow
![]() $h : (m,y) \to (l,z)$
making the following diagram commute:
$h : (m,y) \to (l,z)$
making the following diagram commute:

In fact, such a morphism h exists (not just merely). We may take
![]() ${\mathrm{Fin}(l)}$
to be the coequaliser of f and g, which is a finite set because the relation induced by f and g on
${\mathrm{Fin}(l)}$
to be the coequaliser of f and g, which is a finite set because the relation induced by f and g on
![]() ${\mathrm{Fin}(m)}$
is decidable and the quotient of a finite set by a decidable relation is itself finite. The induced map
${\mathrm{Fin}(m)}$
is decidable and the quotient of a finite set by a decidable relation is itself finite. The induced map
![]() $z : {\mathrm{Fin}(l)} \to X$
follows from the universal property of this coequaliser among sets.
$z : {\mathrm{Fin}(l)} \to X$
follows from the universal property of this coequaliser among sets.
The following example demonstrates that HX may fail to be filtered when X is not a set.
Example 3.3.4 Let
![]() $X := \mathrm{K}({{{\mathbb{Z}}/2},{1}})$
with base point
$X := \mathrm{K}({{{\mathbb{Z}}/2},{1}})$
with base point
![]() $x_0 : X$
. Consider the two parallel arrows in HX:
$x_0 : X$
. Consider the two parallel arrows in HX:

where
![]() $\sigma : \Omega X$
is the non-trivial element under the identification
$\sigma : \Omega X$
is the non-trivial element under the identification
![]() $\Omega X \simeq {\mathbb{Z}} / 2$
. If we had an upper bound
$\Omega X \simeq {\mathbb{Z}} / 2$
. If we had an upper bound
![]() $h : (1, x_0) \to (l, z)$
for these two arrows, then we would obtain an element
$h : (1, x_0) \to (l, z)$
for these two arrows, then we would obtain an element
![]() $p : \Omega X$
such that
$p : \Omega X$
such that
![]() ${\mathrm{\mathtt{refl}}}_{x_0} \centerdot p = \sigma \centerdot p$
. This would imply that
${\mathrm{\mathtt{refl}}}_{x_0} \centerdot p = \sigma \centerdot p$
. This would imply that
![]() ${\mathrm{\mathtt{refl}}}_{x_0} = \sigma$
, which is absurd.
${\mathrm{\mathtt{refl}}}_{x_0} = \sigma$
, which is absurd.
Now we show how to replace diagrams
![]() $ X \to \mathscr{A} $
by diagrams
$ X \to \mathscr{A} $
by diagrams
![]() $ HX \to \mathscr{A} $
.
$ HX \to \mathscr{A} $
.
Construction 3.3.5 We build a functor
![]() $ G : \mathscr{A}^X \to \mathscr{A}^{HX} $
as follows. For a family
$ G : \mathscr{A}^X \to \mathscr{A}^{HX} $
as follows. For a family
![]() $ A : X \to \mathscr{A} $
, define
$ A : X \to \mathscr{A} $
, define
For a morphism
![]() $ (f, p) : (n, x) \to (m, y) $
in HX, we have the path
$ (f, p) : (n, x) \to (m, y) $
in HX, we have the path
![]() $ p : \Pi_{i : {\mathrm{Fin}(n)}} x_i = y_{f(i)} $
which induces a morphism
$ p : \Pi_{i : {\mathrm{Fin}(n)}} x_i = y_{f(i)} $
which induces a morphism
![]() $ A_p : \bigoplus_{i : {\mathrm{Fin}(n)}} A(x_i) \to \bigoplus_{i : {\mathrm{Fin}(n)}} A(y_{f(i)}) $
by transport and functoriality of biproducts. We define the morphism
$ A_p : \bigoplus_{i : {\mathrm{Fin}(n)}} A(x_i) \to \bigoplus_{i : {\mathrm{Fin}(n)}} A(y_{f(i)}) $
by transport and functoriality of biproducts. We define the morphism
![]() $ GA_{(f, p)} : \bigoplus_{i : {\mathrm{Fin}(n)}} A(x_i) \to \bigoplus_{j : {\mathrm{Fin}(m)}} A(y_j) $
as the composite:
$ GA_{(f, p)} : \bigoplus_{i : {\mathrm{Fin}(n)}} A(x_i) \to \bigoplus_{j : {\mathrm{Fin}(m)}} A(y_j) $
as the composite:
where the middle map simply arranges the biproduct using that
![]() ${\mathrm{Fin}(n)}$
is the sum of the fibres of f, and the last map sums over the fibres of f. This sum is well-defined since it is finite: any function between finite types has decidable fibres, and a decidable subset of a finite type is finite; hence,
${\mathrm{Fin}(n)}$
is the sum of the fibres of f, and the last map sums over the fibres of f. This sum is well-defined since it is finite: any function between finite types has decidable fibres, and a decidable subset of a finite type is finite; hence,
![]() $ {\mathrm{fib}_{f}}(j) $
is finite for all
$ {\mathrm{fib}_{f}}(j) $
is finite for all
![]() $ j : {\mathrm{Fin}(m)} $
. We will write
$ j : {\mathrm{Fin}(m)} $
. We will write
![]() $\nabla$
for the composite of the two last maps above. Checking that GA defines a functor is straightforward.
$\nabla$
for the composite of the two last maps above. Checking that GA defines a functor is straightforward.
Lastly, the obvious functor
![]() $ h_X : X \to HX $
defined by
$ h_X : X \to HX $
defined by
![]() $ h_X(x) := (1,x) $
makes the following diagram commute:
$ h_X(x) := (1,x) $
makes the following diagram commute:

The following is the analogue of Harting (Reference Harting1982, Proposition 2.5) in our setting.
Lemma 3.3.6 The functor
![]() $ G : \mathscr{A}^X \to \mathscr{A}^{HX} $
preserves limits.
$ G : \mathscr{A}^X \to \mathscr{A}^{HX} $
preserves limits.
Proof. Let
![]() $ A : \mathscr{D} \to \mathscr{A}^X $
be a diagram whose limit exists. For all
$ A : \mathscr{D} \to \mathscr{A}^X $
be a diagram whose limit exists. For all
![]() $ (n, x) : HX $
, we have
$ (n, x) : HX $
, we have
using that limits in functor categories are computed object-wise, and that
![]() $ \bigoplus_{{\mathrm{Fin}(n)}} $
preserves limits.
$ \bigoplus_{{\mathrm{Fin}(n)}} $
preserves limits.
Before the next proposition, we require a lemma:
Lemma 3.3.7 Let n be a natural number, and let
![]() $ A : X \to \mathscr{A} $
. Consider an object
$ A : X \to \mathscr{A} $
. Consider an object
![]() $ M : \mathscr{A} $
along with a family
$ M : \mathscr{A} $
along with a family
![]() $ \eta : \Pi_{x:X} A(x) \to M $
. For any path
$ \eta : \Pi_{x:X} A(x) \to M $
. For any path
![]() $ p : x = x' $
in
$ p : x = x' $
in
![]() $ X^n $
, the following diagram commutes:
$ X^n $
, the following diagram commutes:

Proof. By path induction on p.
Now we prove that passing between A and GA leaves the colimit unchanged (if it exists).
Proposition 3.3.8 Let
![]() $ A : X \to \mathscr{A} $
. Restriction along the functor
$ A : X \to \mathscr{A} $
. Restriction along the functor
![]() $ h_X : X \to HX $
is an isomorphism
$ h_X : X \to HX $
is an isomorphism
which is natural in
![]() $ M : \mathscr{A} $
. Consequently, the colimits of A and GA coincide, when they exist.
$ M : \mathscr{A} $
. Consequently, the colimits of A and GA coincide, when they exist.
Proof. We construct an explicit inverse e to
![]() $ h_X^* $
. Let
$ h_X^* $
. Let
![]() $ M : \mathscr{A} $
, and let
$ M : \mathscr{A} $
, and let
![]() $ \eta : A \Rightarrow {\mathrm{const}_{X}}(M) $
be a natural transformation, that is, a family
$ \eta : A \Rightarrow {\mathrm{const}_{X}}(M) $
be a natural transformation, that is, a family
![]() $ \eta : \Pi_{x:X} A(x) \to M $
. Given such a family
$ \eta : \Pi_{x:X} A(x) \to M $
. Given such a family
![]() $ \eta $
, we extend it to a natural transformation
$ \eta $
, we extend it to a natural transformation
![]() $ e(\eta) : GA \Rightarrow {\mathrm{const}_{HX}}(M) $
using the biproduct, as follows. For
$ e(\eta) : GA \Rightarrow {\mathrm{const}_{HX}}(M) $
using the biproduct, as follows. For
![]() $ (n, x) : HX $
, let
$ (n, x) : HX $
, let
Thus, we have defined a transformation
![]() $ e(\eta) $
, and now we check naturality.
$ e(\eta) $
, and now we check naturality.
Let
![]() $ (f, p) : (n, x) \to (m, y) $
be a morphism in HX. Our task is to verify that outer triangle in the following diagram commutes:
$ (f, p) : (n, x) \to (m, y) $
be a morphism in HX. Our task is to verify that outer triangle in the following diagram commutes:

where the dashed line is
![]() $ \bigoplus_{i : {\mathrm{Fin}(n)}} \eta_{y_{f(i)}} $
. The inner-left triangle commutes by Lemma 3.3.7. That the inner-right triangle commutes can be immediately checked on each component
$ \bigoplus_{i : {\mathrm{Fin}(n)}} \eta_{y_{f(i)}} $
. The inner-left triangle commutes by Lemma 3.3.7. That the inner-right triangle commutes can be immediately checked on each component
![]() $ i : {\mathrm{Fin}(n)} $
. Thus, we conclude that
$ i : {\mathrm{Fin}(n)} $
. Thus, we conclude that
![]() $ e(\eta) $
is a natural transformation.
$ e(\eta) $
is a natural transformation.
From the construction, it is clear that
![]() $ h_X^* \circ e = {\mathrm{id}}$
. For the other equality, let
$ h_X^* \circ e = {\mathrm{id}}$
. For the other equality, let
![]() $ \nu : GA \Rightarrow {\mathrm{const}_{HX}}(M) $
be a natural transformation. Given some
$ \nu : GA \Rightarrow {\mathrm{const}_{HX}}(M) $
be a natural transformation. Given some
![]() $ (n, x) : HX $
, then for any
$ (n, x) : HX $
, then for any
![]() $ i : {\mathrm{Fin}(n)} $
we have the morphism in HX on the left, whose filler is the reflexivity path:
$ i : {\mathrm{Fin}(n)} $
we have the morphism in HX on the left, whose filler is the reflexivity path:

The vertical arrow in the right triangle is the inclusion, which is also given by functoriality of GA. The right triangle commutes by naturality of
![]() $ \nu $
. By the universal property of the n-fold biproduct, we have that
$ \nu $
. By the universal property of the n-fold biproduct, we have that
![]() $ \nu_{(n,x)} = \bigoplus_{i : {\mathrm{Fin}(n)}} \nu_{(1,x_i)} $
. This means that
$ \nu_{(n,x)} = \bigoplus_{i : {\mathrm{Fin}(n)}} \nu_{(1,x_i)} $
. This means that
![]() $ \nu = e(h_X^*(\nu)) $
, and consequently
$ \nu = e(h_X^*(\nu)) $
, and consequently
![]() $ {\mathrm{id}} = e \circ h_X^* $
.
$ {\mathrm{id}} = e \circ h_X^* $
.
The proposition tells us that the following diagram commutes, whenever
![]() $ \mathscr{A} $
is cocomplete:
$ \mathscr{A} $
is cocomplete:

From this, we deduce the following results.
Corollary 3.3.9 The functor
![]() $ {\mathrm{colim}_{X}} : {{R}\textrm{-}{\mathrm{Mod}}}^X \to {{R}\textrm{-}{\mathrm{Mod}}} $
preserves finite products.
$ {\mathrm{colim}_{X}} : {{R}\textrm{-}{\mathrm{Mod}}}^X \to {{R}\textrm{-}{\mathrm{Mod}}} $
preserves finite products.
Proof. By Lemma 3.3.6, we know that G preserves limits, so we need only argue that
![]() ${\mathrm{colim}_{HX}}$
preserves finite products. Since products of modules are given by products of the underlying sets, and sifted colimits of modules can be computed on the underlying sets by Corollary 2.2.6, this follows from pro:sifted-colimits since HX is sifted (Lemma 3.3.2).
${\mathrm{colim}_{HX}}$
preserves finite products. Since products of modules are given by products of the underlying sets, and sifted colimits of modules can be computed on the underlying sets by Corollary 2.2.6, this follows from pro:sifted-colimits since HX is sifted (Lemma 3.3.2).
Theorem 3.3.10 Suppose
![]() $ \mathscr{A} $
is an abelian category satisfying AB3 and AB5. For any set X, the functor
$ \mathscr{A} $
is an abelian category satisfying AB3 and AB5. For any set X, the functor
![]() $ \bigoplus_X : \mathscr{A}^X \to \mathscr{A} $
is left-exact. In particular,
$ \bigoplus_X : \mathscr{A}^X \to \mathscr{A} $
is left-exact. In particular,
![]() $ \mathscr{A} $
satisfies AB4.
$ \mathscr{A} $
satisfies AB4.
Proof. The assumption that
![]() $ \mathscr{A} $
satisfies AB5 means that the functor
$ \mathscr{A} $
satisfies AB5 means that the functor
![]() $ {\mathrm{colim}_{HX}} $
is exact, because HX is filtered when X is a set by Proposition 3.3.3. Since G preserves limits by Lemma 3.3.6, we conclude from the diagram above that
$ {\mathrm{colim}_{HX}} $
is exact, because HX is filtered when X is a set by Proposition 3.3.3. Since G preserves limits by Lemma 3.3.6, we conclude from the diagram above that
![]() $ {\mathrm{colim}_{X}} $
(that is,
$ {\mathrm{colim}_{X}} $
(that is,
![]() $ \bigoplus_X $
) is left-exact.
$ \bigoplus_X $
) is left-exact.
4 Semantics
We interpret the most central results from the previous sections into an
![]() $ \infty $
-topos
$ \infty $
-topos
![]() $ {\mathscr{X}} $
, as made possible by recent developments on the semantics of HoTT (de Boer, Reference de Boer2020; Kapulkin and Lumsdaine, Reference Kapulkin and Lumsdaine2021; Lumsdaine and Shulman, Reference Lumsdaine and Shulman2020; Shulman, Reference Shulman2019). Specifically, we work out the interpretation of categories of modules (Theorem 4.3.4) and colimits of modules indexed by an object (Theorem 4.3.5).
$ {\mathscr{X}} $
, as made possible by recent developments on the semantics of HoTT (de Boer, Reference de Boer2020; Kapulkin and Lumsdaine, Reference Kapulkin and Lumsdaine2021; Lumsdaine and Shulman, Reference Lumsdaine and Shulman2020; Shulman, Reference Shulman2019). Specifically, we work out the interpretation of categories of modules (Theorem 4.3.4) and colimits of modules indexed by an object (Theorem 4.3.5).
Until now, we have studied categories of abelian groups and modules, as well as abstract abelian categories in HoTT. Semantically, these yield structures in our chosen
![]() $ \infty $
-topos
$ \infty $
-topos
![]() $ {\mathscr{X}} $
. For example, we will see that the ‘internal category’
$ {\mathscr{X}} $
. For example, we will see that the ‘internal category’
![]() $ {\mathrm{\mathtt{Ab}}} $
obtained by interpretation represents – in the sense of Definition 4.1.3 – the presheaf
$ {\mathrm{\mathtt{Ab}}} $
obtained by interpretation represents – in the sense of Definition 4.1.3 – the presheaf
which sends an object
![]() $ X \in {\mathscr{X}} $
to the ordinary category of (relatively
$ X \in {\mathscr{X}} $
to the ordinary category of (relatively
![]() $\kappa$
-compact) abelian groups objects in the 1-topos
$\kappa$
-compact) abelian groups objects in the 1-topos
![]() ${\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})}$
. We often refer to structures in this slice over X just as ‘structures over X’; for example, ‘abelian groups over X’.
${\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})}$
. We often refer to structures in this slice over X just as ‘structures over X’; for example, ‘abelian groups over X’.
We will work and interpret our results directly into the
![]() $\infty$
-topos
$\infty$
-topos
![]() ${\mathscr{X}}$
, justified by the following considerations. Any (Grothendieck)
${\mathscr{X}}$
, justified by the following considerations. Any (Grothendieck)
![]() $ \infty $
-topos
$ \infty $
-topos
![]() $ \mathscr{X} $
can be presented by a type-theoretic model topos
$ \mathscr{X} $
can be presented by a type-theoretic model topos
![]() $\mathscr{M}$
according to Shulman (Reference Shulman2019). Assuming an inaccessible cardinal
$\mathscr{M}$
according to Shulman (Reference Shulman2019). Assuming an inaccessible cardinal
![]() $ \kappa $
, the latter admits a univalent universe for relatively
$ \kappa $
, the latter admits a univalent universe for relatively
![]() $ \kappa $
-presentable fibrations (Shulman, Reference Shulman2019, Definition 4.7) supporting the interpretation of HoTT.
Footnote 1
Constructions in
$ \kappa $
-presentable fibrations (Shulman, Reference Shulman2019, Definition 4.7) supporting the interpretation of HoTT.
Footnote 1
Constructions in
![]() $\mathscr{M}$
present constructions in
$\mathscr{M}$
present constructions in
![]() ${\mathscr{X}}$
, and we are interested in studying our results in the latter. Moreover, Stenzel (to appear) proves that the univalent universe in
${\mathscr{X}}$
, and we are interested in studying our results in the latter. Moreover, Stenzel (to appear) proves that the univalent universe in
![]() $\mathscr{M}$
presents an object classifier
$\mathscr{M}$
presents an object classifier
![]() $ \widetilde{{\mathcal{U}}^\kappa} \to {\mathcal{U}}^\kappa $
(Lurie, Reference Lurie2009, Section 6.1.6) for relatively
$ \widetilde{{\mathcal{U}}^\kappa} \to {\mathcal{U}}^\kappa $
(Lurie, Reference Lurie2009, Section 6.1.6) for relatively
![]() $\kappa$
-compact morphismsFootnote 2 in
$\kappa$
-compact morphismsFootnote 2 in
![]() $ {\mathscr{X}} $
. This means that the universe
$ {\mathscr{X}} $
. This means that the universe
![]() ${\mathcal{U}}^\kappa$
represents the presheaf which maps an object
${\mathcal{U}}^\kappa$
represents the presheaf which maps an object
![]() $X \in {\mathscr{X}}$
to the
$X \in {\mathscr{X}}$
to the
![]() $\infty$
-groupoid
$\infty$
-groupoid
![]() $ {({ {\mathscr{X}} /^\kappa X})^{\simeq}}$
of relatively
$ {({ {\mathscr{X}} /^\kappa X})^{\simeq}}$
of relatively
![]() $\kappa$
-compact maps into X. This makes precise the nature of the univalent universe in
$\kappa$
-compact maps into X. This makes precise the nature of the univalent universe in
![]() ${\mathscr{X}}$
corresponding to the one from HoTT, and we will not need to refer to
${\mathscr{X}}$
corresponding to the one from HoTT, and we will not need to refer to
![]() $\mathscr{M}$
from here on. We mention that Vergura (Reference Vergura2019) gives another example of working out the interpretation of material in HoTT directly into an
$\mathscr{M}$
from here on. We mention that Vergura (Reference Vergura2019) gives another example of working out the interpretation of material in HoTT directly into an
![]() $\infty$
-topos. However, our case is simpler because we mainly work with truncated objects.
$\infty$
-topos. However, our case is simpler because we mainly work with truncated objects.
We will require a small fragment of the theory of complete Segal objects (Rasekh, Reference Rasekh2018) in
![]() $ {\mathscr{X}} $
(also called internal
$ {\mathscr{X}} $
(also called internal
![]() $\infty $
-categories Martini Reference Martini2021 or Rezk objects Riehl and Verity Reference Riehl and Verity2022). As our model of the (large)
$\infty $
-categories Martini Reference Martini2021 or Rezk objects Riehl and Verity Reference Riehl and Verity2022). As our model of the (large)
![]() $ \infty $
-category
$ \infty $
-category
![]() $ {\mathrm{Cat}_\infty} $
of
$ {\mathrm{Cat}_\infty} $
of
![]() $ \infty $
-categories, we choose the
$ \infty $
-categories, we choose the
![]() $ \infty $
-category of complete Segal spaces. Though our arguments will clearly be model-independent, certain constructions require a choice, and this is a convenient one for our purposes.
$ \infty $
-category of complete Segal spaces. Though our arguments will clearly be model-independent, certain constructions require a choice, and this is a convenient one for our purposes.
Notation We write
![]() $ {\mathscr{X}_{\kappa}} $
for the sub-
$ {\mathscr{X}_{\kappa}} $
for the sub-
![]() $\infty$
-category of
$\infty$
-category of
![]() $ \kappa $
-compact objects in
$ \kappa $
-compact objects in
![]() $ {\mathscr{X}} $
, and for an object
$ {\mathscr{X}} $
, and for an object
![]() $ X \in {\mathscr{X}} $
we form the slice
$ X \in {\mathscr{X}} $
we form the slice
![]() $ {\mathscr{X}} /^\kappa X $
of relatively
$ {\mathscr{X}} /^\kappa X $
of relatively
![]() $ \kappa $
-compact morphisms into X. The 1-topos of 0-truncated objects in
$ \kappa $
-compact morphisms into X. The 1-topos of 0-truncated objects in
![]() $ {\mathscr{X}} $
is
$ {\mathscr{X}} $
is
![]() $ {\tau_{\leq 0}({{\mathscr{X}}})} $
. The functor
$ {\tau_{\leq 0}({{\mathscr{X}}})} $
. The functor
![]() $ {(-)^{\simeq}} : {\mathrm{Cat}_\infty} \to {\mathscr{S}} $
picks out the
$ {(-)^{\simeq}} : {\mathrm{Cat}_\infty} \to {\mathscr{S}} $
picks out the
![]() $ \infty $
-groupoid core of an
$ \infty $
-groupoid core of an
![]() $ \infty $
-category, and
$ \infty $
-category, and
![]() $ {\mathscr{S}} $
is the
$ {\mathscr{S}} $
is the
![]() $ \infty $
-category of spaces (also called
$ \infty $
-category of spaces (also called
![]() $\infty$
-groupoids). For complete Segal spaces, the functor
$\infty$
-groupoids). For complete Segal spaces, the functor
![]() $ {(-)^{\simeq}} $
simply picks out the zeroth space. The classifier for
$ {(-)^{\simeq}} $
simply picks out the zeroth space. The classifier for
![]() $\kappa$
-compact morphisms in
$\kappa$
-compact morphisms in
![]() $ {\mathscr{X}} $
presented by Shulman’s univalent universe will be written
$ {\mathscr{X}} $
presented by Shulman’s univalent universe will be written
![]() $ {\widetilde{{\mathcal{U}}}} \to {\mathcal{U}} $
, leaving
$ {\widetilde{{\mathcal{U}}}} \to {\mathcal{U}} $
, leaving
![]() $ \kappa $
implicit. No confusion will arise as no other universes will be around. Internal homs are written using exponential notation
$ \kappa $
implicit. No confusion will arise as no other universes will be around. Internal homs are written using exponential notation
![]() $Y^X$
.
$Y^X$
.
Notions in
![]() $ {\mathscr{X}} $
resulting from interpretation will be denoted in typewriter font. For example, we will be considering the universe
$ {\mathscr{X}} $
resulting from interpretation will be denoted in typewriter font. For example, we will be considering the universe
![]() $ {\mathrm{\mathtt{Set}}} $
which classifies
$ {\mathrm{\mathtt{Set}}} $
which classifies
![]() $\kappa$
-compact 0-truncated objects (Lemma 4.2.2). In particular, we leave the
$\kappa$
-compact 0-truncated objects (Lemma 4.2.2). In particular, we leave the
![]() $ \kappa $
implicit in the notation of the universe of sets (or of abelian groups or of R-modules).
$ \kappa $
implicit in the notation of the universe of sets (or of abelian groups or of R-modules).
The 1-category
![]() $\Delta_{\leq 2}$
is the full subcategory of the simplex category
$\Delta_{\leq 2}$
is the full subcategory of the simplex category
![]() $\Delta$
on the objects [0], [1] and [2]. The
$\Delta$
on the objects [0], [1] and [2]. The
![]() $\infty$
-category of (
$\infty$
-category of (
![]() $\infty$
-)functors
$\infty$
-)functors
![]() ${\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}}$
consists of 2-restricted simplicial objects in
${\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}}$
consists of 2-restricted simplicial objects in
![]() ${\mathscr{X}}$
and is denoted
${\mathscr{X}}$
and is denoted
![]() ${\mathscr{X}}_{{\Delta_{\leq 2}}}$
for short. We explain how we view 1-categories as
${\mathscr{X}}_{{\Delta_{\leq 2}}}$
for short. We explain how we view 1-categories as
![]() $\infty$
-categories just below. The standard n-simplex is the usual simplicial space
$\infty$
-categories just below. The standard n-simplex is the usual simplicial space
![]() $\Delta^n : {\Delta^{\mathrm{op}}} \to {\mathscr{S}}$
and its 2-restriction is
$\Delta^n : {\Delta^{\mathrm{op}}} \to {\mathscr{S}}$
and its 2-restriction is
![]() ${\Delta}_{\leq 2}^n : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{S}}$
. There is also a standard n-simplex
${\Delta}_{\leq 2}^n : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{S}}$
. There is also a standard n-simplex
![]() $\underline{\Delta}^n$
in
$\underline{\Delta}^n$
in
![]() ${\mathscr{X}}$
, whose 2-restriction we denote
${\mathscr{X}}$
, whose 2-restriction we denote
![]() ${\underline{\Delta}}_{\leq 2}^n : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}}$
.
${\underline{\Delta}}_{\leq 2}^n : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}}$
.
4.1 Rezk (1,1)(1,1)-objects
The first goal of this section is to repackage the internal categories in
![]() $ {\mathscr{X}} $
obtained by interpretation into structures which conveniently represent presheaves of 1-categories. We begin by explaining how we assign 1-categories to
$ {\mathscr{X}} $
obtained by interpretation into structures which conveniently represent presheaves of 1-categories. We begin by explaining how we assign 1-categories to
![]() $ \infty $
-categories akin to
$ \infty $
-categories akin to
![]() $ {\mathscr{X}} $
. An ordinary category
$ {\mathscr{X}} $
. An ordinary category
![]() $ {\mathscr{C}} $
is incarnated as a simplicial space through its classifying diagram
$ {\mathscr{C}} $
is incarnated as a simplicial space through its classifying diagram
![]() $ \mathrm{D}({\mathscr{C}}) $
(Rezk, Reference Rezk2001, Section 3.5):
$ \mathrm{D}({\mathscr{C}}) $
(Rezk, Reference Rezk2001, Section 3.5):

where we used
![]() $ {(-)^{\simeq}} $
to denote the Kan complex obtained from the groupoid core of a 1-category, and [n] denotes the usual poset with
$ {(-)^{\simeq}} $
to denote the Kan complex obtained from the groupoid core of a 1-category, and [n] denotes the usual poset with
![]() $ n+1 $
elements. This classifying diagram is a complete Segal space, and there is a Quillen adjunction
$ n+1 $
elements. This classifying diagram is a complete Segal space, and there is a Quillen adjunction
![]() $ {\mathrm{h}} : {\mathrm{Cat}_\infty} \leftrightarrows {\mathrm{Cat}} : \mathrm{D} $
which exhibits
$ {\mathrm{h}} : {\mathrm{Cat}_\infty} \leftrightarrows {\mathrm{Cat}} : \mathrm{D} $
which exhibits
![]() $ {\mathrm{Cat}} $
as precisely the 1-truncated complete Segal spaces (Campbell and Lanari, Reference Campbell and Lanari2020, Theorem 5.11). The left adjoint
$ {\mathrm{Cat}} $
as precisely the 1-truncated complete Segal spaces (Campbell and Lanari, Reference Campbell and Lanari2020, Theorem 5.11). The left adjoint
![]() $ {\mathrm{h}} $
is the fundamental category functor. We view ordinary 1-categories as
$ {\mathrm{h}} $
is the fundamental category functor. We view ordinary 1-categories as
![]() $\infty$
-categories via this construction, and by identifying
$\infty$
-categories via this construction, and by identifying
![]() $ {\mathrm{Cat}} $
with its image under the embedding
$ {\mathrm{Cat}} $
with its image under the embedding
![]() $ \mathrm{D} $
, we may speak about presheaves of 1-categories on
$ \mathrm{D} $
, we may speak about presheaves of 1-categories on
![]() ${\mathscr{X}}$
.
${\mathscr{X}}$
.
We will argue that precategories and categories in HoTT interpret to the following structures.
Definition 4.1.1. A Segal (1,1) -object in
![]() $ {\mathscr{X}} $
is a 2-restricted simplicial object
$ {\mathscr{X}} $
is a 2-restricted simplicial object
![]() $ {\mathscr{C}} : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}} $
satisfying the three following conditions:
$ {\mathscr{C}} : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}} $
satisfying the three following conditions:
(truncation) the structure map
![]() $ ({\mathrm{dom}}, \mathrm{cod}) : {\mathscr{C}}_1 \to {\mathscr{C}}_0 \times {\mathscr{C}}_0 $
is 0-truncated in
$ ({\mathrm{dom}}, \mathrm{cod}) : {\mathscr{C}}_1 \to {\mathscr{C}}_0 \times {\mathscr{C}}_0 $
is 0-truncated in
![]() $ {\mathscr{X}} $
;
$ {\mathscr{X}} $
;
(Segal condition) the natural map
![]() $ {\mathscr{C}}_2 \to {\mathscr{C}}_1 \times_{{\mathscr{C}}_0} {\mathscr{C}}_1 $
is an equivalence;
$ {\mathscr{C}}_2 \to {\mathscr{C}}_1 \times_{{\mathscr{C}}_0} {\mathscr{C}}_1 $
is an equivalence;
(associativity) there is a witness that the following two composites agree:

where
![]() $ \circ : {\mathscr{C}}_1 \times_{{\mathscr{C}}_0} {\mathscr{C}}_1 \xrightarrow{\sim} {\mathscr{C}}_2 \xrightarrow{\delta^2_1} {\mathscr{C}}_1 $
.
$ \circ : {\mathscr{C}}_1 \times_{{\mathscr{C}}_0} {\mathscr{C}}_1 \xrightarrow{\sim} {\mathscr{C}}_2 \xrightarrow{\delta^2_1} {\mathscr{C}}_1 $
.
If moreover the square below is a pullback, then
![]() $ {\mathscr{C}} $
is a Rezk (1,1)-object:
$ {\mathscr{C}} $
is a Rezk (1,1)-object:

The Segal (or Rezk) (1,1)-object
![]() $ {\mathscr{C}} $
is locally small if the structure map is relatively
$ {\mathscr{C}} $
is locally small if the structure map is relatively
![]() $\kappa$
-compact.
$\kappa$
-compact.
We emphasise that the truncation condition on the structure maps implies that there is at most one witness of associativity (meaning it is a property).
It is straightforward to interpret Definition 9.1.1 from The Univalent Foundations Program (2013) to see what the datum of a precategory in
![]() $ {\mathscr{X}} $
consists of. We allow the underlying type of a precategory to be any object of
$ {\mathscr{X}} $
consists of. We allow the underlying type of a precategory to be any object of
![]() $ {\mathscr{X}} $
, not necessarily classified by
$ {\mathscr{X}} $
, not necessarily classified by
![]() $ {\mathcal{U}} $
. Our next lemma gives a precise relation between precategories in
$ {\mathcal{U}} $
. Our next lemma gives a precise relation between precategories in
![]() ${\mathscr{X}}$
and the structures just defined.
${\mathscr{X}}$
and the structures just defined.
Lemma 4.1.2 Precategories in
![]() $ {\mathscr{X}} $
correspond to locally small Segal (1,1)-objects and categories to locally small Rezk (1,1)-objects.
$ {\mathscr{X}} $
correspond to locally small Segal (1,1)-objects and categories to locally small Rezk (1,1)-objects.
Here, by ‘correspond’ we mean that from one structure one can construct the other, and vice-versa. In particular, we may apply results about (pre)categories in HoTT to (Segal) Rezk (1,1)-objects in
![]() ${\mathscr{X}}$
. However, we are not constructing an equivalence of spaces (or objects) of such structures (though there may well be one).
${\mathscr{X}}$
. However, we are not constructing an equivalence of spaces (or objects) of such structures (though there may well be one).
Proof. Given a precategory
![]() $ {\mathrm{\mathtt{C}}} $
, we define a 2-restricted simplicial object
$ {\mathrm{\mathtt{C}}} $
, we define a 2-restricted simplicial object
![]() $ {\mathrm{\mathtt{C}}}_\bullet $
as follows. Let
$ {\mathrm{\mathtt{C}}}_\bullet $
as follows. Let
![]() $ {\mathrm{\mathtt{C}}}_0 := {\mathrm{\mathtt{C}}} $
, and write
$ {\mathrm{\mathtt{C}}}_0 := {\mathrm{\mathtt{C}}} $
, and write
![]() $ ({\mathrm{dom}}, \mathrm{cod}) : {\mathrm{\mathtt{C}}}_1 \to {\mathrm{\mathtt{C}}}_0 \times {\mathrm{\mathtt{C}}}_0 $
for the total space of the hom
$ ({\mathrm{dom}}, \mathrm{cod}) : {\mathrm{\mathtt{C}}}_1 \to {\mathrm{\mathtt{C}}}_0 \times {\mathrm{\mathtt{C}}}_0 $
for the total space of the hom
![]() $ {\mathrm{\mathtt{C}}}(-,-) : {\mathrm{\mathtt{C}}} \times {\mathrm{\mathtt{C}}} \to {\mathrm{\mathtt{Set}}} $
with its projection. The identity maps
$ {\mathrm{\mathtt{C}}}(-,-) : {\mathrm{\mathtt{C}}} \times {\mathrm{\mathtt{C}}} \to {\mathrm{\mathtt{Set}}} $
with its projection. The identity maps
![]() $ {\mathrm{id}} : \Pi_{c : {\mathrm{\mathtt{C}}}} {\mathrm{\mathtt{C}}}(c,c) $
give a section
$ {\mathrm{id}} : \Pi_{c : {\mathrm{\mathtt{C}}}} {\mathrm{\mathtt{C}}}(c,c) $
give a section
![]() $ {\mathrm{\mathtt{C}}}_0 \to {\mathrm{\mathtt{C}}}_1 $
of both
$ {\mathrm{\mathtt{C}}}_0 \to {\mathrm{\mathtt{C}}}_1 $
of both
![]() $ {\mathrm{dom}} $
and
$ {\mathrm{dom}} $
and
![]() $ \mathrm{cod} $
. Now let
$ \mathrm{cod} $
. Now let
![]() $ {\mathrm{\mathtt{C}}}_2 := \Sigma_{a, b, c : {\mathrm{\mathtt{C}}}_0} \Sigma_{f : {\mathrm{\mathtt{C}}}(a,b)} \Sigma_{g : {\mathrm{\mathtt{C}}}(b,c)} \Sigma_{h : {\mathrm{\mathtt{C}}}(a,c)} gf = h $
be the object of commuting triangles in
$ {\mathrm{\mathtt{C}}}_2 := \Sigma_{a, b, c : {\mathrm{\mathtt{C}}}_0} \Sigma_{f : {\mathrm{\mathtt{C}}}(a,b)} \Sigma_{g : {\mathrm{\mathtt{C}}}(b,c)} \Sigma_{h : {\mathrm{\mathtt{C}}}(a,c)} gf = h $
be the object of commuting triangles in
![]() $ {\mathrm{\mathtt{C}}} $
. Then,
$ {\mathrm{\mathtt{C}}} $
. Then,
![]() $ {\mathrm{\mathtt{C}}}_\bullet $
is a 2-restricted simplicial object in
$ {\mathrm{\mathtt{C}}}_\bullet $
is a 2-restricted simplicial object in
![]() $ {\mathscr{X}} $
with face maps given by projections, and degeneracies induced by
$ {\mathscr{X}} $
with face maps given by projections, and degeneracies induced by
![]() $ {\mathrm{id}} $
. Clearly
$ {\mathrm{id}} $
. Clearly
![]() $ {\mathrm{\mathtt{C}}}_\bullet $
satisfies the truncation condition and is associative (since the precategory
$ {\mathrm{\mathtt{C}}}_\bullet $
satisfies the truncation condition and is associative (since the precategory
![]() ${\mathrm{\mathtt{C}}}$
is). In HoTT, it is easy to show that the map
${\mathrm{\mathtt{C}}}$
is). In HoTT, it is easy to show that the map
![]() $ (f, g) \mapsto (f,g,gf, {\mathrm{\mathtt{refl}}}_{gf}) $
is inverse to the natural map
$ (f, g) \mapsto (f,g,gf, {\mathrm{\mathtt{refl}}}_{gf}) $
is inverse to the natural map
![]() $ {\mathrm{\mathtt{C}}}_2 \to {\mathrm{\mathtt{C}}}_1 \times_{{\mathrm{\mathtt{C}}}_0} {\mathrm{\mathtt{C}}}_1 $
; thus, we conclude that
$ {\mathrm{\mathtt{C}}}_2 \to {\mathrm{\mathtt{C}}}_1 \times_{{\mathrm{\mathtt{C}}}_0} {\mathrm{\mathtt{C}}}_1 $
; thus, we conclude that
![]() $ {\mathrm{\mathtt{C}}}_\bullet $
is a Segal (1,1)-object. It is locally small by construction.
$ {\mathrm{\mathtt{C}}}_\bullet $
is a Segal (1,1)-object. It is locally small by construction.
It is similarly straightforward to produce a precategory from a locally small Segal (1,1)-object. Under this correspondence, univalence of a precategory is equivalent to the square (2) being a pullback, so we conclude that categories correspond to Rezk (1,1)-objects.
Now we explain in what sense Rezk (1,1)-objects represent presheaves of ordinary categories. It is clear that to recover the fundamental category of a classifying diagram it suffices to recover the lower three simplicial levels. This leads us to the following notion of representability.
Definition 4.1.3 Let
![]() $ {\mathscr{C}} : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}} $
be a presheaf of 1 -categories on
$ {\mathscr{C}} : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}} $
be a presheaf of 1 -categories on
![]() $ {\mathscr{X}} $
. A Rezk (1,1)-object
$ {\mathscr{X}} $
. A Rezk (1,1)-object
![]() $ {\mathrm{\mathtt{C}}} : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}} $
represents
$ {\mathrm{\mathtt{C}}} : {\Delta_{\leq 2}^{\mathrm{op}}} \to {\mathscr{X}} $
represents
![]() $ {\mathscr{C}} $
if there is a specified natural equivalence
$ {\mathscr{C}} $
if there is a specified natural equivalence
![]() $ \eta : {\mathscr{X}}(-,{\mathrm{\mathtt{C}}}_\bullet) \simeq i^*_2 {\mathscr{C}} $
of functors
$ \eta : {\mathscr{X}}(-,{\mathrm{\mathtt{C}}}_\bullet) \simeq i^*_2 {\mathscr{C}} $
of functors
![]() $ {\mathscr{X}}^{\mathrm{op}} \to {\mathscr{S}}_{\Delta_{\leq 2}} $
, where
$ {\mathscr{X}}^{\mathrm{op}} \to {\mathscr{S}}_{\Delta_{\leq 2}} $
, where
![]() $ i^*_2 $
is the restriction along the inclusion
$ i^*_2 $
is the restriction along the inclusion
![]() $ \Delta_{\leq 2} \to \Delta $
.
$ \Delta_{\leq 2} \to \Delta $
.
We will use this notion of representability when working out the semantics of the category of sets and categories of modules in the next sections. The reader who is mainly interested in those representability results (such as Theorem 4.3.4) may skip ahead to the next section. The remaining parts of this section are only needed for Theorem 4.3.5.
Any statement about (pre)categories in HoTT yields a statement about locally small (Segal) Rezk (1,1)-objects by translating across the correspondence of Lemma 4.1.2. For example, one can check that products of (pre)categories correspond to object-wise products of (Segal) Rezk (1,1)-objects. Our next statement is that functor precategories interpret to the internal hom of Segal (1,1)-objects.
If
![]() $ F, G : \mathscr{C} \to \mathscr{D} $
are two functors between (pre)categories in HoTT, then we can represent natural transformations
$ F, G : \mathscr{C} \to \mathscr{D} $
are two functors between (pre)categories in HoTT, then we can represent natural transformations
![]() $ F \Rightarrow G $
as functors
$ F \Rightarrow G $
as functors
![]() $ \eta : \mathscr{C} \times [1] \to \mathscr{D} $
such that
$ \eta : \mathscr{C} \times [1] \to \mathscr{D} $
such that
![]() $ \eta \lvert_{\mathscr{C} \times \{0\}} = F $
and
$ \eta \lvert_{\mathscr{C} \times \{0\}} = F $
and
![]() $ \eta \lvert_{\mathscr{C} \times \{1 \}} = G $
. Here, [n] denotes the usual precategory (poset) in HoTT with
$ \eta \lvert_{\mathscr{C} \times \{1 \}} = G $
. Here, [n] denotes the usual precategory (poset) in HoTT with
![]() $n+1$
elements. The precategory [n] interprets to the Segal (1,1)-object
$n+1$
elements. The precategory [n] interprets to the Segal (1,1)-object
![]() $\underline{\Delta}_{\leq 2}^n$
which is the 2-restriction of the standard n-simplex
$\underline{\Delta}_{\leq 2}^n$
which is the 2-restriction of the standard n-simplex
![]() $ \underline{\Delta}^n : {\Delta^{\mathrm{op}}} \to {\mathscr{X}} $
in
$ \underline{\Delta}^n : {\Delta^{\mathrm{op}}} \to {\mathscr{X}} $
in
![]() ${\mathscr{X}}$
.
${\mathscr{X}}$
.
We have the following:
Lemma 4.1.4 Let
![]() $ {\mathscr{C}} $
and
$ {\mathscr{C}} $
and
![]() $ {\mathscr{D}} $
be locally small Segal (1,1)-objects in
$ {\mathscr{D}} $
be locally small Segal (1,1)-objects in
![]() $ {\mathscr{X}} $
.
$ {\mathscr{X}} $
.
-
(1) The object of functors
 $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}}) $
obtained by interpretation represents the presheaf where the base change functor
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}}) $
obtained by interpretation represents the presheaf where the base change functor \[ X \longmapsto ({\mathscr{X}} / X)_{\Delta_{\leq 2}}(X \times {\mathscr{C}}, X \times {\mathscr{D}}) \ : \ {\mathscr{X}}^{\mathrm{op}} \longrightarrow {\mathscr{S}} \]
\[ X \longmapsto ({\mathscr{X}} / X)_{\Delta_{\leq 2}}(X \times {\mathscr{C}}, X \times {\mathscr{D}}) \ : \ {\mathscr{X}}^{\mathrm{op}} \longrightarrow {\mathscr{S}} \]
 $ X \times (-) $
is applied object-wise.
$ X \times (-) $
is applied object-wise.
-
(2) The Segal (1,1)-object
 $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
obtained by interpreting the functor category is equivalent to where the degeneracy and face maps come from the
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
obtained by interpreting the functor category is equivalent to where the degeneracy and face maps come from the
 $ \underline{\Delta}_{\leq 2}^n $
’s. If
$ \underline{\Delta}_{\leq 2}^n $
’s. If
 $ {\mathscr{D}} $
is Rezk, then so is
$ {\mathscr{D}} $
is Rezk, then so is
 $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
.
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
.
Proof. It is straightforward to see that functors between precategories in HoTT interpret to simplicial maps between the corresponding Segal (1,1)-objects. Then, (1) follows by stability of interpretation across base change.
By representing natural transformations as functors, we see that
![]() $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}} \times \underline{\Delta}_{\leq 2}^1, {\mathscr{D}}) $
is the total space of the map
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}} \times \underline{\Delta}_{\leq 2}^1, {\mathscr{D}}) $
is the total space of the map
![]() $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})^2 \to {\mathrm{\mathtt{Set}}} $
which sends two functors to the set of natural transformations between them. Thus, we get the first and second levels of (2). Finally, the third level is naturally equivalent to
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})^2 \to {\mathrm{\mathtt{Set}}} $
which sends two functors to the set of natural transformations between them. Thus, we get the first and second levels of (2). Finally, the third level is naturally equivalent to
![]() $ {{\mathrm{\mathtt{Fun}}}}(\underline{\Delta}_{\leq 2}^2, {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet) $
in HoTT, and the latter is clearly equivalent to the space of commuting triangles in
$ {{\mathrm{\mathtt{Fun}}}}(\underline{\Delta}_{\leq 2}^2, {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet) $
in HoTT, and the latter is clearly equivalent to the space of commuting triangles in
![]() $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}}) $
. These equivalences assemble to a simplicial map, so we are done.
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}}) $
. These equivalences assemble to a simplicial map, so we are done.
We note that by combining part (1) and (2) of the lemma, we get a formula for the presheaf represented by
![]() $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
.
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
.
When working with Segal and Rezk (1,1)-objects, we may use category-theoretical language as long as the relevant interpretation has been worked out or is apparent from the context. We also note that we can take
![]() $ {\mathscr{X}} $
to be the
$ {\mathscr{X}} $
to be the
![]() $\infty$
-topos
$\infty$
-topos
![]() $ {\mathscr{S}} $
of spaces, and in this case we will use the terminology Segal and Rezk (1,1)-spaces for emphasis.
$ {\mathscr{S}} $
of spaces, and in this case we will use the terminology Segal and Rezk (1,1)-spaces for emphasis.
Our next proposition asserts that functor categories interpret to the internal hom in
![]() $ {\mathscr{X}}_{\Delta_{\leq 2}} $
. To prove this, we require a lemma. First recall the terminal geometric morphism
$ {\mathscr{X}}_{\Delta_{\leq 2}} $
. To prove this, we require a lemma. First recall the terminal geometric morphism
![]() $ {\mathscr{X}}(1, -) : {\mathscr{X}} \to {\mathscr{S}} $
(with left adjoint
$ {\mathscr{X}}(1, -) : {\mathscr{X}} \to {\mathscr{S}} $
(with left adjoint
![]() $\ell$
) associated with any
$\ell$
) associated with any
![]() $\infty$
-topos. Applying this adjunction object-wise, we get an induced adjunction
$\infty$
-topos. Applying this adjunction object-wise, we get an induced adjunction
The left-exactness of
![]() $ \ell_* $
implies that it preserves Segal and Rezk (1,1)-objects. Moreover, since
$ \ell_* $
implies that it preserves Segal and Rezk (1,1)-objects. Moreover, since
![]() $\ell_*$
preserves finite limits and colimits, it preserves the standard n-simplex so that we have
$\ell_*$
preserves finite limits and colimits, it preserves the standard n-simplex so that we have
![]() $\ell_*(\Delta_{\leq 2}^n) = \underline{\Delta}_{\leq 2}^n$
.
$\ell_*(\Delta_{\leq 2}^n) = \underline{\Delta}_{\leq 2}^n$
.
Lemma 4.1.5 Let
![]() $ {\mathscr{C}}, {\mathscr{D}} \in {\mathscr{X}}_{\Delta_{\leq 2}} $
. For
$ {\mathscr{C}}, {\mathscr{D}} \in {\mathscr{X}}_{\Delta_{\leq 2}} $
. For
![]() $ X \in {\mathscr{X}} $
and
$ X \in {\mathscr{X}} $
and
![]() $ n \in \{ 0, 1, 2 \} $
, we have natural equivalences
$ n \in \{ 0, 1, 2 \} $
, we have natural equivalences
Proof. By stability of the internal hom across base change, we can assume
![]() $ X = 1 $
. We then have
$ X = 1 $
. We then have
where the first equivalence is by cartesian-closedness of
![]() $ {\mathscr{X}}_{\Delta_{\leq 2}} $
, the second equivalence comes from the adjunction
$ {\mathscr{X}}_{\Delta_{\leq 2}} $
, the second equivalence comes from the adjunction
![]() $ \ell_* \dashv {\mathscr{X}}(1,-) $
and that
$ \ell_* \dashv {\mathscr{X}}(1,-) $
and that
![]() $\ell_*(\Delta_{\leq 2}^n) = \underline{\Delta}_{\leq 2}^n$
. The last equivalence is by the Yoneda lemma.
$\ell_*(\Delta_{\leq 2}^n) = \underline{\Delta}_{\leq 2}^n$
. The last equivalence is by the Yoneda lemma.
Proposition 4.1.6
Let
![]() $ {\mathscr{C}} $
and
$ {\mathscr{C}} $
and
![]() $ {\mathscr{D}} $
be locally small Segal (1,1)-objects in
$ {\mathscr{D}} $
be locally small Segal (1,1)-objects in
![]() $ {\mathscr{X}} $
. The 2-restricted simplicial objects
$ {\mathscr{X}} $
. The 2-restricted simplicial objects
![]() ${{\mathscr{D}}^{{\mathscr{C}}}}$
and
${{\mathscr{D}}^{{\mathscr{C}}}}$
and
![]() $ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
in
$ {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}})_\bullet $
in
![]() $ {\mathscr{X}} $
are naturally equivalent.
$ {\mathscr{X}} $
are naturally equivalent.
Proof. By the Yoneda lemma, it suffices to show that the functors
![]() $ {\mathscr{X}}(-, {\mathscr{D}}^{\mathscr{C}}) $
and
$ {\mathscr{X}}(-, {\mathscr{D}}^{\mathscr{C}}) $
and
![]() $ {\mathscr{X}}(-, {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}}))_\bullet $
of the form
$ {\mathscr{X}}(-, {{\mathrm{\mathtt{Fun}}}}({\mathscr{C}}, {\mathscr{D}}))_\bullet $
of the form
![]() $ {\mathscr{X}}^{\mathrm{op}} \to {\mathscr{S}}_{\Delta_{\leq 2}} $
are equivalent. This follows by combining the two previous lemmas.
$ {\mathscr{X}}^{\mathrm{op}} \to {\mathscr{S}}_{\Delta_{\leq 2}} $
are equivalent. This follows by combining the two previous lemmas.
The proposition implies that the internal hom between Segal (1,1)-objects is itself a Segal (1,1)-object, and even Rezk if the codomain is.
If
![]() $ {\mathscr{C}} $
is a Rezk (1,1)-object in
$ {\mathscr{C}} $
is a Rezk (1,1)-object in
![]() $ {\mathscr{X}} $
, then the internal limit of a functor
$ {\mathscr{X}} $
, then the internal limit of a functor
![]() $ F : {\mathscr{D}} \to {\mathscr{C}} $
in
$ F : {\mathscr{D}} \to {\mathscr{C}} $
in
![]() $ {\mathscr{X}}_{\Delta_{\leq 2}} $
defines a global point
$ {\mathscr{X}}_{\Delta_{\leq 2}} $
defines a global point
![]() $ {{\mathrm{\mathtt{lim}}}_{{\mathscr{D}}}} F \in {\mathscr{X}}(1,{\mathscr{C}}_0) $
, if the internal limit exists. Of course, so does the limit of an external functor
$ {{\mathrm{\mathtt{lim}}}_{{\mathscr{D}}}} F \in {\mathscr{X}}(1,{\mathscr{C}}_0) $
, if the internal limit exists. Of course, so does the limit of an external functor
![]() $ G : D \to {\mathscr{X}}(1,{\mathscr{C}}) $
in
$ G : D \to {\mathscr{X}}(1,{\mathscr{C}}) $
in
![]() $ {\mathscr{S}}_{{\Delta_{\leq 2}}} $
. We now explain how such external functors
$ {\mathscr{S}}_{{\Delta_{\leq 2}}} $
. We now explain how such external functors
![]() $ D \to {\mathscr{X}}(1,{\mathscr{C}}) $
can be internalised to functors in
$ D \to {\mathscr{X}}(1,{\mathscr{C}}) $
can be internalised to functors in
![]() ${\mathscr{X}}_{\Delta_{\leq 2}}$
, and we prove that this procedure does not change the limit or colimit.
${\mathscr{X}}_{\Delta_{\leq 2}}$
, and we prove that this procedure does not change the limit or colimit.
Definition 4.1.7 Let
![]() $ {\mathscr{C}} $
be a Rezk (1,1)-object in
$ {\mathscr{C}} $
be a Rezk (1,1)-object in
![]() $ {\mathscr{X}} $
, and D a Rezk (1,1)-space. The internalisation of a functor
$ {\mathscr{X}} $
, and D a Rezk (1,1)-space. The internalisation of a functor
![]() $ A : D \to {\mathscr{X}}(1,{\mathscr{C}}) $
is its transpose
$ A : D \to {\mathscr{X}}(1,{\mathscr{C}}) $
is its transpose
![]() $ \underline{A} : \ell_*(D) \to {\mathscr{C}} $
across the adjunction
$ \underline{A} : \ell_*(D) \to {\mathscr{C}} $
across the adjunction
![]() $ \ell_* \dashv {\mathscr{X}}(1,-) $
.
$ \ell_* \dashv {\mathscr{X}}(1,-) $
.
To show that internalisation of a functor does not change its (co)limit, we require a lemma. The reader may find it interesting to compare it with Johnstone (Reference Johnstone1977, Example 2.39).
Lemma 4.1.8 Let
![]() $ {\mathscr{C}} $
be a Rezk (1,1)-object in
$ {\mathscr{C}} $
be a Rezk (1,1)-object in
![]() $ {\mathscr{X}} $
, and D a Rezk (1,1)-space. The Rezk (1,1)-spaces
$ {\mathscr{X}} $
, and D a Rezk (1,1)-space. The Rezk (1,1)-spaces
![]() $ {\mathscr{X}}(1, {\mathscr{C}}^{\ell_*(D)}) $
and
$ {\mathscr{X}}(1, {\mathscr{C}}^{\ell_*(D)}) $
and
![]() $ {\mathscr{X}}(1,{\mathscr{C}})^D $
are naturally equivalent.
$ {\mathscr{X}}(1,{\mathscr{C}})^D $
are naturally equivalent.
Proof. Using Lemma 4.1.5 and the adjunction
![]() $ \ell_* \dashv {\mathscr{X}}(1,-) $
, for
$ \ell_* \dashv {\mathscr{X}}(1,-) $
, for
![]() $ n \in \{0,1,2\} $
we have
$ n \in \{0,1,2\} $
we have
where the second equivalence uses that
![]() $ \ell_* $
preserves products (being left-exact) and then transposes across the adjunction. The third equivalence is Lemma 4.1.5 applied to Rezk (1,1)-spaces. Using basic properties of adjunctions, one can check that these equivalences assemble to a simplicial map.
$ \ell_* $
preserves products (being left-exact) and then transposes across the adjunction. The third equivalence is Lemma 4.1.5 applied to Rezk (1,1)-spaces. Using basic properties of adjunctions, one can check that these equivalences assemble to a simplicial map.
The category of sets in HoTT interprets to a Rezk (1,1)-object
![]() $ {\mathrm{\mathtt{Set}}}_\bullet $
which features in the next proposition, and is the main topic of study in the next section. For the following proof, we only use that
$ {\mathrm{\mathtt{Set}}}_\bullet $
which features in the next proposition, and is the main topic of study in the next section. For the following proof, we only use that
![]() $ {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}_\bullet) $
has a terminal object and therefore a global sections functor
$ {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}_\bullet) $
has a terminal object and therefore a global sections functor
![]() $ \Gamma : {\mathscr{X}}(1, {\mathrm{\mathtt{Set}}}_\bullet) \to {{\tau_{\leq 0}({{\mathscr{S}}})}} $
. Observe that if
$ \Gamma : {\mathscr{X}}(1, {\mathrm{\mathtt{Set}}}_\bullet) \to {{\tau_{\leq 0}({{\mathscr{S}}})}} $
. Observe that if
![]() $ {\mathscr{C}} $
is a Rezk (1,1)-object in
$ {\mathscr{C}} $
is a Rezk (1,1)-object in
![]() $ {\mathscr{X}} $
, then the Rezk (1,1)-space
$ {\mathscr{X}} $
, then the Rezk (1,1)-space
![]() $ {\mathscr{X}}(1,{\mathscr{C}}) $
is enriched over
$ {\mathscr{X}}(1,{\mathscr{C}}) $
is enriched over
![]() $ {\mathscr{X}}(1, {\mathrm{\mathtt{Set}}}_\bullet) $
. A study of this enrichment is beyond the scope of this work, and our convention will be to implicitly apply
$ {\mathscr{X}}(1, {\mathrm{\mathtt{Set}}}_\bullet) $
. A study of this enrichment is beyond the scope of this work, and our convention will be to implicitly apply
![]() $ \Gamma $
so that the hom functor
$ \Gamma $
so that the hom functor
![]() $ {\mathscr{X}}(1,{\mathscr{C}})(-,-) $
lands in
$ {\mathscr{X}}(1,{\mathscr{C}})(-,-) $
lands in
![]() $ {{\tau_{\leq 0}({{\mathscr{S}}})}} $
.
$ {{\tau_{\leq 0}({{\mathscr{S}}})}} $
.
Proposition 4.1.9 Let
![]() $ {\mathscr{C}} $
be a locally small Rezk (1,1)-object in
$ {\mathscr{C}} $
be a locally small Rezk (1,1)-object in
![]() $ {\mathscr{X}} $
, and let
$ {\mathscr{X}} $
, and let
![]() $ A : D \to {\mathscr{X}}(1,{\mathscr{C}}) $
be a functor between Rezk (1,1)-spaces. If the internal limit
$ A : D \to {\mathscr{X}}(1,{\mathscr{C}}) $
be a functor between Rezk (1,1)-spaces. If the internal limit
![]() $ {{\mathrm{\mathtt{lim}}}_{\ell_*(D)}} \underline{A} $
in
$ {{\mathrm{\mathtt{lim}}}_{\ell_*(D)}} \underline{A} $
in
![]() $ {\mathscr{C}} $
exists, so does the limit of A and we have a canonical isomorphism
$ {\mathscr{C}} $
exists, so does the limit of A and we have a canonical isomorphism
![]() $ {{\mathrm{\mathtt{lim}}}_{\ell_*(D)}} \underline{A} \simeq {\mathrm{lim}_{{D}}}\, A $
in
$ {{\mathrm{\mathtt{lim}}}_{\ell_*(D)}} \underline{A} \simeq {\mathrm{lim}_{{D}}}\, A $
in
![]() $ {\mathscr{X}}(1,{\mathscr{C}}) $
.
$ {\mathscr{X}}(1,{\mathscr{C}}) $
.
Proof. Suppose the internal limit of
![]() $ \underline{A} $
in
$ \underline{A} $
in
![]() $ {\mathscr{C}} $
exists, giving an equivalence of functors
$ {\mathscr{C}} $
exists, giving an equivalence of functors
![]() $ {\mathscr{C}}^{\mathrm{op}} \to {\mathrm{\mathtt{Set}}}_\bullet $
$ {\mathscr{C}}^{\mathrm{op}} \to {\mathrm{\mathtt{Set}}}_\bullet $
Applying
![]() $ {\mathscr{X}}(1, -) $
, we get an equivalence between certain functors
$ {\mathscr{X}}(1, -) $
, we get an equivalence between certain functors
![]() $ {\mathscr{X}}(1,{\mathscr{C}})^{\mathrm{op}} \to {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}_\bullet) $
, and by further post-composing with the global sections map
$ {\mathscr{X}}(1,{\mathscr{C}})^{\mathrm{op}} \to {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}_\bullet) $
, and by further post-composing with the global sections map
![]() $ \Gamma : {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}_\bullet) \to {{\tau_{\leq 0}({{\mathscr{S}}})}} $
, we get an equivalence
$ \Gamma : {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}_\bullet) \to {{\tau_{\leq 0}({{\mathscr{S}}})}} $
, we get an equivalence
between functors
![]() $ {\mathscr{X}}(1,{\mathscr{C}})^{\mathrm{op}} \to {{\tau_{\leq 0}({{\mathscr{S}}})}} $
. We have an equivalence
$ {\mathscr{X}}(1,{\mathscr{C}})^{\mathrm{op}} \to {{\tau_{\leq 0}({{\mathscr{S}}})}} $
. We have an equivalence
![]() $ {\mathscr{X}}(1, {\mathscr{C}}^{\ell_*(D)}) \simeq {\mathscr{X}}(1,{\mathscr{C}})^D $
by the previous lemma, which sends
$ {\mathscr{X}}(1, {\mathscr{C}}^{\ell_*(D)}) \simeq {\mathscr{X}}(1,{\mathscr{C}})^D $
by the previous lemma, which sends
![]() $ {{\mathrm{\mathtt{const}}}_{\ell_*(D)}} $
to
$ {{\mathrm{\mathtt{const}}}_{\ell_*(D)}} $
to
![]() $ {\mathrm{const}_{D}} $
and
$ {\mathrm{const}_{D}} $
and
![]() $ \underline{A} $
to A. On hom-spaces, this means we have
$ \underline{A} $
to A. On hom-spaces, this means we have
Combining the equivalences (3) and (4), we see that
![]() $ {{\mathrm{\mathtt{lim}}}_{\ell_*(D)}} \underline{A} $
is the limit of A, as desired.
$ {{\mathrm{\mathtt{lim}}}_{\ell_*(D)}} \underline{A} $
is the limit of A, as desired.
The proposition and its proof dualises to colimits, but we will only need it for limits.
4.2 The universe of sets
We show that the Rezk (1,1)-object
![]() $ {\mathrm{\mathtt{Set}}}_\bullet $
produced by interpretation represents the presheaf
$ {\mathrm{\mathtt{Set}}}_\bullet $
produced by interpretation represents the presheaf
![]() $ {\tau_{\leq 0}({{\mathscr{X}} /^\kappa (-)})} : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}} $
in the sense of Definition 4.1.3. First we show a lemma that proves useful for these kinds of representability results.
$ {\tau_{\leq 0}({{\mathscr{X}} /^\kappa (-)})} : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}} $
in the sense of Definition 4.1.3. First we show a lemma that proves useful for these kinds of representability results.
The universe
![]() $ {\mathcal{U}} $
is an object classifier for relatively
$ {\mathcal{U}} $
is an object classifier for relatively
![]() $\kappa$
-compact morphisms (Stenzel, toappear) in the sense of Lurie (Reference Lurie2009, Section 6.1.6) and therefore represents (in the usual sense) the presheaf
$\kappa$
-compact morphisms (Stenzel, toappear) in the sense of Lurie (Reference Lurie2009, Section 6.1.6) and therefore represents (in the usual sense) the presheaf
![]() $ {({{\mathscr{X}} /^\kappa (-)})^{\simeq}} : {\mathscr{X}}^{\mathrm{op}} \to {\mathscr{S}} $
. We will be interested in types which classify certain structures in
$ {({{\mathscr{X}} /^\kappa (-)})^{\simeq}} : {\mathscr{X}}^{\mathrm{op}} \to {\mathscr{S}} $
. We will be interested in types which classify certain structures in
![]() $ {\mathscr{X}} $
. For example, given a ring
$ {\mathscr{X}} $
. For example, given a ring
![]() $ R \in {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
, we will see that there is a map
$ R \in {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
, we will see that there is a map
![]() $ {\mathrm{\mathtt{R{-}mod{-}str}}} : {\mathrm{\mathtt{Set}}} \to {\mathcal{U}} $
which classifies R-modules in
$ {\mathrm{\mathtt{R{-}mod{-}str}}} : {\mathrm{\mathtt{Set}}} \to {\mathcal{U}} $
which classifies R-modules in
![]() $ {\mathscr{X}_{\kappa}} $
, meaning that the mapping space
$ {\mathscr{X}_{\kappa}} $
, meaning that the mapping space
![]() $ {\mathscr{X}}\big(X, \Sigma_{A:{\mathrm{\mathtt{Set}}}} {\mathrm{\mathtt{R{-}mod{-}str}}}(A)\big) $
is the groupoid of R-modules in
$ {\mathscr{X}}\big(X, \Sigma_{A:{\mathrm{\mathtt{Set}}}} {\mathrm{\mathtt{R{-}mod{-}str}}}(A)\big) $
is the groupoid of R-modules in
![]() $ ({\mathscr{X}} /^\kappa X) $
(Theorem 4.3.4). The following lemma gives a description of these mapping spaces for general type families.
$ ({\mathscr{X}} /^\kappa X) $
(Theorem 4.3.4). The following lemma gives a description of these mapping spaces for general type families.
Lemma 4.2.1 Let
![]() $ P : Z \to {\mathcal{U}} $
be a type family in
$ P : Z \to {\mathcal{U}} $
be a type family in
![]() $ {\mathscr{X}} $
, and
$ {\mathscr{X}} $
, and
![]() $ X \in {\mathscr{X}} $
. The outer square in the following diagram is a pullback:
$ X \in {\mathscr{X}} $
. The outer square in the following diagram is a pullback:

where the functor
![]() $ {{\Gamma}^{\simeq}} $
is the restriction of the global points functor
$ {{\Gamma}^{\simeq}} $
is the restriction of the global points functor
![]() $ \Gamma : ({\mathscr{X}} /^\kappa X) \to {\mathscr{S}} $
to the core, and
$ \Gamma : ({\mathscr{X}} /^\kappa X) \to {\mathscr{S}} $
to the core, and
![]() $ ({\mathscr{X}} /^\kappa X)_* $
is the
$ ({\mathscr{X}} /^\kappa X)_* $
is the
![]() $\infty$
-category of relatively
$\infty$
-category of relatively
![]() $\kappa$
-compact maps into X equipped with a section.
$\kappa$
-compact maps into X equipped with a section.
Proof. The right square is manifestly a pullback, and so is the left square since
![]() $ {\mathscr{X}}(X,-) $
preserves limits. The middle square is a pullback because
$ {\mathscr{X}}(X,-) $
preserves limits. The middle square is a pullback because
![]() $ {\widetilde{{\mathcal{U}}}} $
classifies pointed objects. By pullback pasting, we conclude that the outer square is a pullback.
$ {\widetilde{{\mathcal{U}}}} $
classifies pointed objects. By pullback pasting, we conclude that the outer square is a pullback.
Recall that
![]() $ {\mathrm{\mathtt{Set}}} $
is defined as the total space of the map
$ {\mathrm{\mathtt{Set}}} $
is defined as the total space of the map
![]() $ {\mathrm{\mathtt{is{-}0{-}type}}} : {\mathcal{U}} \to {\mathcal{U}} $
sending an object A to the proposition that the diagonal map
$ {\mathrm{\mathtt{is{-}0{-}type}}} : {\mathcal{U}} \to {\mathcal{U}} $
sending an object A to the proposition that the diagonal map
![]() $A \to A \times A$
is an embedding (or
$A \to A \times A$
is an embedding (or
![]() $(-1)$
-truncated). By Lurie (Reference Lurie2009, Lemma 5.5.6.15), this proposition holds (i.e., has a global point) if and only if A is 0-truncated (meaning that
$(-1)$
-truncated). By Lurie (Reference Lurie2009, Lemma 5.5.6.15), this proposition holds (i.e., has a global point) if and only if A is 0-truncated (meaning that
![]() ${\mathscr{X}}(B,A)$
is a 0-truncated space for all
${\mathscr{X}}(B,A)$
is a 0-truncated space for all
![]() $B \in {\mathscr{X}}$
Lurie Reference Lurie2009, Definition 5.5.6.1). We now show that the universe
$B \in {\mathscr{X}}$
Lurie Reference Lurie2009, Definition 5.5.6.1). We now show that the universe
![]() $ {\mathrm{\mathtt{Set}}} $
of sets classifies 0-truncated objects:
$ {\mathrm{\mathtt{Set}}} $
of sets classifies 0-truncated objects:
Lemma 4.2.2 The object
![]() $ {\mathrm{\mathtt{Set}}} $
represents the presheaf of spaces
$ {\mathrm{\mathtt{Set}}} $
represents the presheaf of spaces
![]() $ {{{\tau_{\leq 0}({{\mathscr{X}} /^\kappa (-)})}}^{\simeq}} $
.
$ {{{\tau_{\leq 0}({{\mathscr{X}} /^\kappa (-)})}}^{\simeq}} $
.
Proof. By applying the previous lemma to the type family
![]() $ {\mathrm{\mathtt{is{-}0{-}type}}} : {\mathcal{U}} \to {\mathcal{U}} $
, we see that
$ {\mathrm{\mathtt{is{-}0{-}type}}} : {\mathcal{U}} \to {\mathcal{U}} $
, we see that
![]() $ {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}) $
is the sub-
$ {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}) $
is the sub-
![]() $\infty$
-groupoid of
$\infty$
-groupoid of
![]() $ {\mathscr{X}}(1,{\mathcal{U}}) $
on those objects
$ {\mathscr{X}}(1,{\mathcal{U}}) $
on those objects
![]() $ A : {\mathcal{U}} $
for which
$ A : {\mathcal{U}} $
for which
![]() $ {\mathrm{\mathtt{is{-}0{-}type}}}(A) $
holds. Since
$ {\mathrm{\mathtt{is{-}0{-}type}}}(A) $
holds. Since
![]() $ {\mathrm{\mathtt{is{-}0{-}type}}}(A) $
holds if and only if A is 0-truncated,
$ {\mathrm{\mathtt{is{-}0{-}type}}}(A) $
holds if and only if A is 0-truncated,
![]() $ {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}) $
is equivalent to the groupoid of 0-truncated objects in
$ {\mathscr{X}}(1,{\mathrm{\mathtt{Set}}}) $
is equivalent to the groupoid of 0-truncated objects in
![]() $ {\mathscr{X}_{\kappa}} $
.
$ {\mathscr{X}_{\kappa}} $
.
For general X, we always have that families
![]() $ X \to {\mathrm{\mathtt{Set}}} $
correspond to families
$ X \to {\mathrm{\mathtt{Set}}} $
correspond to families
![]() $ X \to X \times {\mathrm{\mathtt{Set}}} $
over X. Base change stability of the universe implies that
$ X \to X \times {\mathrm{\mathtt{Set}}} $
over X. Base change stability of the universe implies that
![]() $ X \times {\mathrm{\mathtt{Set}}} $
is a universe of sets in
$ X \times {\mathrm{\mathtt{Set}}} $
is a universe of sets in
![]() $ {\mathscr{X}} / X $
. Thus, we reduce to the case
$ {\mathscr{X}} / X $
. Thus, we reduce to the case
![]() $ X = 1 $
just treated by pulling back over X, using that an arrow
$ X = 1 $
just treated by pulling back over X, using that an arrow
![]() $f : Y \to X$
is 0-truncated as a map if and only if it is 0-truncated as an object of
$f : Y \to X$
is 0-truncated as a map if and only if it is 0-truncated as an object of
![]() ${\mathscr{X}} / X$
(Lurie, Reference Lurie2009, Remark 5.5.6.12).
${\mathscr{X}} / X$
(Lurie, Reference Lurie2009, Remark 5.5.6.12).
Our next goal is to understand the presheaf represented by
![]() ${\mathrm{\mathtt{Set}}}$
when equipped with its categorical structure. Applying (Rasekh, Reference Rasekh2021, Theorem 4.4) to the universal map
${\mathrm{\mathtt{Set}}}$
when equipped with its categorical structure. Applying (Rasekh, Reference Rasekh2021, Theorem 4.4) to the universal map
![]() $ p : {\widetilde{{\mathcal{U}}}} \to {\mathcal{U}} $
yields a complete Segal object N(p) in
$ p : {\widetilde{{\mathcal{U}}}} \to {\mathcal{U}} $
yields a complete Segal object N(p) in
![]() $ {\mathscr{X}} $
which represents (in the usual sense) the presheaf
$ {\mathscr{X}} $
which represents (in the usual sense) the presheaf
![]() $ ({\mathscr{X}} /^\kappa (-)) : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}_\infty} $
. The 2-restriction of N(p) is equivalent to the following 2-restricted simplicial object
$ ({\mathscr{X}} /^\kappa (-)) : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}_\infty} $
. The 2-restriction of N(p) is equivalent to the following 2-restricted simplicial object
![]() $ {\mathcal{U}}_\bullet $
in
$ {\mathcal{U}}_\bullet $
in
![]() $ {\mathscr{X}} $
:
$ {\mathscr{X}} $
:
To be explicit, we know that the function types modelled by the universe interpret to the internal hom in
![]() $ {\mathscr{X}} $
, so the first simplicial level is simply the type-theoretic notation for Rasekh’s description of
$ {\mathscr{X}} $
, so the first simplicial level is simply the type-theoretic notation for Rasekh’s description of
![]() $ N(p)_1 $
, and the second level is given by the Segal condition. Accordingly, for the Rezk (1,1)-object
$ N(p)_1 $
, and the second level is given by the Segal condition. Accordingly, for the Rezk (1,1)-object
![]() $ {\mathrm{\mathtt{Set}}}_\bullet $
, the object of morphisms is simply given by internal homs in
$ {\mathrm{\mathtt{Set}}}_\bullet $
, the object of morphisms is simply given by internal homs in
![]() $ {\mathscr{X}} $
:
$ {\mathscr{X}} $
:
The following provides the semantics of the category of sets in HoTT.
Proposition 4.2.3 The Rezk (1,1)-object
![]() $ {\mathrm{\mathtt{Set}}}_\bullet $
represents the presheaf
$ {\mathrm{\mathtt{Set}}}_\bullet $
represents the presheaf
![]() $ {\tau_{\leq 0}({{\mathscr{X}} /^\kappa (-)})} : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}} $
in the sense of Definition 4.1.3.
$ {\tau_{\leq 0}({{\mathscr{X}} /^\kappa (-)})} : {\mathscr{X}}^{\mathrm{op}} \to {\mathrm{Cat}} $
in the sense of Definition 4.1.3.
Proof. Let
![]() $ X \in {\mathscr{X}} $
. We need to produce a natural equivalence
$ X \in {\mathscr{X}} $
. We need to produce a natural equivalence
![]() $ \eta : {\mathscr{X}}(X,{\mathrm{\mathtt{Set}}}_\bullet) \simeq i^*_2 ({\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})}) $
of 2-restricted simplicial spaces. By Lemma 4.2.2, we get a natural equivalence of the zeroth levels. Since the global points of the internal hom give the external hom, Lemma 4.2.1 tells us that
$ \eta : {\mathscr{X}}(X,{\mathrm{\mathtt{Set}}}_\bullet) \simeq i^*_2 ({\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})}) $
of 2-restricted simplicial spaces. By Lemma 4.2.2, we get a natural equivalence of the zeroth levels. Since the global points of the internal hom give the external hom, Lemma 4.2.1 tells us that
![]() $ {\mathscr{X}}(X,{\mathrm{\mathtt{Set}}}_1) $
is naturally equivalent to the groupoid of arrows in
$ {\mathscr{X}}(X,{\mathrm{\mathtt{Set}}}_1) $
is naturally equivalent to the groupoid of arrows in
![]() $ {\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})} $
. These two equivalences clearly assemble to an equivalence of 1-restricted simplicial objects, whereby we get an induced equivalence of the second simplicial levels via the Segal condition. The latter equivalence automatically respects the face maps
$ {\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})} $
. These two equivalences clearly assemble to an equivalence of 1-restricted simplicial objects, whereby we get an induced equivalence of the second simplicial levels via the Segal condition. The latter equivalence automatically respects the face maps
![]() $ \delta^2_0 $
and
$ \delta^2_0 $
and
![]() $ \delta^2_2 $
as well as the degeneracies. It remains to check that it respects the composition map
$ \delta^2_2 $
as well as the degeneracies. It remains to check that it respects the composition map
![]() $ \delta^2_1 $
. But this follows from the fact that function types interpret to the internal hom in
$ \delta^2_1 $
. But this follows from the fact that function types interpret to the internal hom in
![]() $ {\mathscr{X}} $
.
$ {\mathscr{X}} $
.
Before making analogous considerations for the universe of modules, we make these results more concrete by relating them to classical 1-topos theory. These considerations are certainly well known.
By definition, any
![]() $\infty$
-topos
$\infty$
-topos
![]() ${\mathscr{X}}$
is an accessible, left-exact localisation of an
${\mathscr{X}}$
is an accessible, left-exact localisation of an
![]() $\infty$
-category of
$\infty$
-category of
![]() $\infty$
-presheaves on some site. The following proposition shows that the associated 1-topos
$\infty$
-presheaves on some site. The following proposition shows that the associated 1-topos
![]() ${\tau_{\leq 0}({{\mathscr{X}}})}$
of 0-truncated sheaves consists precisely of those sheaves which take values in sets. Thus, if
${\tau_{\leq 0}({{\mathscr{X}}})}$
of 0-truncated sheaves consists precisely of those sheaves which take values in sets. Thus, if
![]() ${\mathscr{C}}$
is an ordinary 1-category (with a site structure), then
${\mathscr{C}}$
is an ordinary 1-category (with a site structure), then
![]() ${\tau_{\leq 0}({{\mathscr{X}}})}$
is the ordinary 1-topos of sheaves of sets on
${\tau_{\leq 0}({{\mathscr{X}}})}$
is the ordinary 1-topos of sheaves of sets on
![]() ${\mathscr{C}}$
. (We also note that the proof works for general truncation levels, but we only use the case
${\mathscr{C}}$
. (We also note that the proof works for general truncation levels, but we only use the case
![]() $n = 0$
.)
$n = 0$
.)
Proposition 4.2.4 Let
![]() $L : {\mathrm{Psh}_\infty(\mathscr{C})} \leftrightarrows {\mathscr{X}} : i$
be an accessible, left-exact localisation for some
$L : {\mathrm{Psh}_\infty(\mathscr{C})} \leftrightarrows {\mathscr{X}} : i$
be an accessible, left-exact localisation for some
![]() $\infty$
-category
$\infty$
-category
![]() ${\mathscr{C}}$
. An object
${\mathscr{C}}$
. An object
![]() $X \in {\mathscr{X}}$
is 0-truncated if and only if X(c) is 0-truncated for all
$X \in {\mathscr{X}}$
is 0-truncated if and only if X(c) is 0-truncated for all
![]() $c \in {\mathscr{C}}$
.
$c \in {\mathscr{C}}$
.
Proof. The statement for presheaves is shown in nLab authors (2023, Proposition 4.2). Let
![]() $X : {\mathscr{C}}^{\mathrm{op}} \to {\mathscr{S}}$
be an element of
$X : {\mathscr{C}}^{\mathrm{op}} \to {\mathscr{S}}$
be an element of
![]() ${\mathscr{X}}$
. First we suppose that X takes values in
${\mathscr{X}}$
. First we suppose that X takes values in
![]() ${\tau_{\leq 0}({{\mathscr{S}}})}$
. Thus, i(X) is a 0-truncated presheaf, by the claim for presheaves. Since L commutes with truncation (Lurie, Reference Lurie2009, Proposition 5.5.6.28), we conclude that
${\tau_{\leq 0}({{\mathscr{S}}})}$
. Thus, i(X) is a 0-truncated presheaf, by the claim for presheaves. Since L commutes with truncation (Lurie, Reference Lurie2009, Proposition 5.5.6.28), we conclude that
![]() $X \simeq L(i(X))$
is also 0-truncated.
$X \simeq L(i(X))$
is also 0-truncated.
Conversely, suppose that X is 0-truncated. Then the space
![]() ${\mathscr{X}}(Y,X)$
is 0-truncated for all
${\mathscr{X}}(Y,X)$
is 0-truncated for all
![]() $Y \in {\mathscr{X}}$
. For any
$Y \in {\mathscr{X}}$
. For any
![]() $c \in {\mathscr{C}}$
, the Yoneda lemma and the adjunction
$c \in {\mathscr{C}}$
, the Yoneda lemma and the adjunction
![]() $L \dashv i$
give us equivalences
$L \dashv i$
give us equivalences
Thus, the leftmost side is 0-truncated, since the rightmost side is.
4.3 The universe of R-modules
Let R be a ring object in
![]() $ {\tau_{\leq 0}({{\mathscr{X}}})} $
. We show that the Rezk (1,1)-object
$ {\tau_{\leq 0}({{\mathscr{X}}})} $
. We show that the Rezk (1,1)-object
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_\bullet $
of R-modules in
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_\bullet $
of R-modules in
![]() $ {\mathscr{X}} $
represents the presheaf sending an object
$ {\mathscr{X}} $
represents the presheaf sending an object
![]() $ X \in {\mathscr{X}} $
to the ordinary category of modules over the ring
$ X \in {\mathscr{X}} $
to the ordinary category of modules over the ring
![]() $ X \times R$
in the 1-topos
$ X \times R$
in the 1-topos
![]() ${\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})} $
(Theorem 4.3.4).
${\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})} $
(Theorem 4.3.4).
The key ingredient we used to prove that
![]() $ {\mathrm{\mathtt{Set}}} $
classifies 0-truncated objects was that
$ {\mathrm{\mathtt{Set}}} $
classifies 0-truncated objects was that
![]() $ {\mathrm{\mathtt{is{-}0{-}type}}}(A) $
has a global point if and only if A is a 0-truncated object. Similarly, to say what
$ {\mathrm{\mathtt{is{-}0{-}type}}}(A) $
has a global point if and only if A is a 0-truncated object. Similarly, to say what
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
classifies we need to understand the global points of
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
classifies we need to understand the global points of
![]() $ {\mathrm{\mathtt{R{-}mod{-}str}}}(A) $
.
$ {\mathrm{\mathtt{R{-}mod{-}str}}}(A) $
.
Lemma 4.3.1 Let R be a ring object in
![]() $ {\tau_{\leq 0}({{\mathscr{X}}})} $
. For all
$ {\tau_{\leq 0}({{\mathscr{X}}})} $
. For all
![]() $ A \in {\tau_{\leq 0}({{\mathscr{X}}})} $
, global points of the object
$ A \in {\tau_{\leq 0}({{\mathscr{X}}})} $
, global points of the object
![]() $ \mathrm{\mathtt{R{-}mod{-}str}}(A) $
biject with R-module structures on the object A in
$ \mathrm{\mathtt{R{-}mod{-}str}}(A) $
biject with R-module structures on the object A in
![]() $ {\mathscr{X}} $
.
$ {\mathscr{X}} $
.
Proof. It is well known that the global points of A,
![]() $ A^A $
,
$ A^A $
,
![]() $A^{A \times A} $
and
$A^{A \times A} $
and
![]() $ A^{R \times A} $
biject, respectively, with the set of points of A, the set of endomorphisms of A, the set of binary operations on A and set of maps
$ A^{R \times A} $
biject, respectively, with the set of points of A, the set of endomorphisms of A, the set of binary operations on A and set of maps
![]() $ R \times A \to A $
in
$ R \times A \to A $
in
![]() $ {\tau_{\leq 0}({{\mathscr{X}}})} $
. One can check the global points functor
$ {\tau_{\leq 0}({{\mathscr{X}}})} $
. One can check the global points functor
![]() $ \Gamma $
sends the limit diagram carving out the subobject
$ \Gamma $
sends the limit diagram carving out the subobject
![]() $ \mathrm{\mathtt{R{-}mod{-}str}}(A) $
of internal R-module structures on A to the limit diagram carving out the (external) set of R-module structures on A from inside the set
$ \mathrm{\mathtt{R{-}mod{-}str}}(A) $
of internal R-module structures on A to the limit diagram carving out the (external) set of R-module structures on A from inside the set
Since
![]() $ \Gamma $
preserves limits, we are done.
$ \Gamma $
preserves limits, we are done.
For a ring
![]() $ R \in {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
and an object
$ R \in {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
and an object
![]() $ X \in {\mathscr{X}} $
, recall that
$ X \in {\mathscr{X}} $
, recall that
![]() $ X {\times} R \in {\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})} $
is a ring over X. We now show that
$ X {\times} R \in {\tau_{\leq 0}({{\mathscr{X}} /^\kappa X})} $
is a ring over X. We now show that
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
classifies R-modules in
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
classifies R-modules in
![]() $ {\mathscr{X}_{\kappa}} $
.
$ {\mathscr{X}_{\kappa}} $
.
Proposition 4.3.2 Let R be a ring in
![]() $ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
. The object
$ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
. The object
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
represents the space-valued presheaf
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
represents the space-valued presheaf
Proof. First of all, for any
![]() $X \in {\mathscr{X}}$
, base change stability of the universe gives
$X \in {\mathscr{X}}$
, base change stability of the universe gives
![]() $ {{(X{\times}R)}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} \simeq X \times {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
over X. From this, we deduce the following natural equivalences:
$ {{(X{\times}R)}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} \simeq X \times {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
over X. From this, we deduce the following natural equivalences:
By working with the rightmost space, we reduce to the case
![]() $X = 1$
.
$X = 1$
.
As defined,
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
is the total space of
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}} $
is the total space of
![]() $ \mathrm{\mathtt{R{-}mod{-}str}} $
. Combining Lemmas 4.3.1 and 4.2.1, we see that
$ \mathrm{\mathtt{R{-}mod{-}str}} $
. Combining Lemmas 4.3.1 and 4.2.1, we see that
![]() $ {\mathscr{X}}(1,{{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}) $
is naturally equivalent to the groupoid of R-modules in
$ {\mathscr{X}}(1,{{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}) $
is naturally equivalent to the groupoid of R-modules in
![]() $ {\mathscr{X}_{\kappa}} $
, as desired.
$ {\mathscr{X}_{\kappa}} $
, as desired.
We recall how internal objects of homomorphisms in
![]() $ {\mathscr{X}} $
are constructed. Given an abelian group object A in
$ {\mathscr{X}} $
are constructed. Given an abelian group object A in
![]() ${\tau_{\leq 0}({{\mathscr{X}}})}$
, we write
${\tau_{\leq 0}({{\mathscr{X}}})}$
, we write
![]() $+_A : A \times A \to A$
for the addition map.
$+_A : A \times A \to A$
for the addition map.
Definition 4.3.3
-
(1) Let A and B be abelian group objects in
 $ {\tau_{\leq 0}({{\mathscr{X}}})} $
. The object of group homomorphisms
$ {\tau_{\leq 0}({{\mathscr{X}}})} $
. The object of group homomorphisms
 $ {\underline{\mathrm{Ab}}}(A,B) $
is the following equaliser in
$ {\underline{\mathrm{Ab}}}(A,B) $
is the following equaliser in
 $ {\mathscr{X}} $
:
$ {\mathscr{X}} $
: 
-
(2) Let R be a ring in
 $ {\tau_{\leq 0}({{\mathscr{X}}})} $
, and let A and B be two R-modules. Write
$ {\tau_{\leq 0}({{\mathscr{X}}})} $
, and let A and B be two R-modules. Write
 $ \alpha_X : R \times X \to X $
for the R-action on an R-module X. The object of R-module morphisms
$ \alpha_X : R \times X \to X $
for the R-action on an R-module X. The object of R-module morphisms
 $ {R{\textrm{-}}\underline{\mathrm{Mod}}}(A,B) $
is the following equaliser in
$ {R{\textrm{-}}\underline{\mathrm{Mod}}}(A,B) $
is the following equaliser in
 $ {\mathscr{X}} $
:
$ {\mathscr{X}} $
: 
It is not hard to see, using an argument similar to the proof of Lemma 4.3.1, that the global points of
![]() $ {R{\textrm{-}}\underline{\mathrm{Mod}}}(A,B) $
are actual R-module homomorphisms from A to B. In addition, the object
$ {R{\textrm{-}}\underline{\mathrm{Mod}}}(A,B) $
are actual R-module homomorphisms from A to B. In addition, the object
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}(A,B) $
coming from interpretation is equivalent to
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}(A,B) $
coming from interpretation is equivalent to
![]() $ {R{\textrm{-}}\underline{\mathrm{Mod}}}(A,B) $
, since it interprets to the same equaliser.
$ {R{\textrm{-}}\underline{\mathrm{Mod}}}(A,B) $
, since it interprets to the same equaliser.
Theorem 4.3.4 Let R be a ring in
![]() $ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
. The Rezk (1,1)-object
$ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
. The Rezk (1,1)-object
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_\bullet $
represents the presheaf
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_\bullet $
represents the presheaf
in the sense of Definition 4.1.3.
Proof. Let
![]() $ X \in {\mathscr{X}} $
. By our definition of representability, we need to produce a natural equivalence
$ X \in {\mathscr{X}} $
. By our definition of representability, we need to produce a natural equivalence
![]() $ \eta : {\mathscr{X}}(X,{{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_\bullet) \simeq i^*_2 {{(X{\times}R)}\textrm{-}{\mathrm{Mod}}} $
of 2-restricted simplicial spaces, and Proposition 4.3.2 gets us
$ \eta : {\mathscr{X}}(X,{{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_\bullet) \simeq i^*_2 {{(X{\times}R)}\textrm{-}{\mathrm{Mod}}} $
of 2-restricted simplicial spaces, and Proposition 4.3.2 gets us
![]() $ \eta_0 $
.
$ \eta_0 $
.
For the first level, recall that
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_1 $
is the total space of the family
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_1 $
is the total space of the family
![]() $ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}(-,-) : {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}^2 \to {\mathrm{\mathtt{Ab}}} $
in
$ {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}(-,-) : {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}^2 \to {\mathrm{\mathtt{Ab}}} $
in
![]() ${\mathscr{X}}$
. By our discussion just above, applying
${\mathscr{X}}$
. By our discussion just above, applying
![]() $ {\mathscr{X}}(X,-) $
to this family recovers the internal hom of
$ {\mathscr{X}}(X,-) $
to this family recovers the internal hom of
![]() $(X{\times}R)$
-modules restricted to the groupoid core: Since the global points of the internal hom of modules recovers the external hom of modules, Lemma 4.2.1 gives a natural equivalence of spaces
$(X{\times}R)$
-modules restricted to the groupoid core: Since the global points of the internal hom of modules recovers the external hom of modules, Lemma 4.2.1 gives a natural equivalence of spaces
By construction, this equivalence respects the two projection maps sending a homomorphism to its domain and codomain. We also need to check that
![]() $\eta_1$
respects the degeneracy map
$\eta_1$
respects the degeneracy map
which picks out the identity. This follows from the corresponding fact for sets, since
![]() $ {\mathrm{id}} $
here is induced by the degeneracy
$ {\mathrm{id}} $
here is induced by the degeneracy
![]() $ {\mathscr{X}}(X,{\mathrm{\mathtt{Set}}}) \to {\mathscr{X}}(X, {\mathrm{\mathtt{Set}}}_1) $
and equality of R -module homomorphisms can be checked on the underlying maps. We conclude that
$ {\mathscr{X}}(X,{\mathrm{\mathtt{Set}}}) \to {\mathscr{X}}(X, {\mathrm{\mathtt{Set}}}_1) $
and equality of R -module homomorphisms can be checked on the underlying maps. We conclude that
![]() $ \eta_0 $
and
$ \eta_0 $
and
![]() $ \eta_1 $
assemble to a map of 1 -restricted simplicial spaces.
$ \eta_1 $
assemble to a map of 1 -restricted simplicial spaces.
For the second level, we have a candidate equivalence for
![]() $ \eta_2 : {\mathscr{X}}(X,{{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_2) \to {({{{R}\textrm{-}{\mathrm{Mod}}}^{[2]}})^{\simeq}} $
given by
$ \eta_2 : {\mathscr{X}}(X,{{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}_2) \to {({{{R}\textrm{-}{\mathrm{Mod}}}^{[2]}})^{\simeq}} $
given by
![]() $ \eta_1 \times_{\eta_0} \eta_1 $
using the Segal condition and that
$ \eta_1 \times_{\eta_0} \eta_1 $
using the Segal condition and that
![]() $ {\mathscr{X}}(X,-) $
preserves limits. By construction,
$ {\mathscr{X}}(X,-) $
preserves limits. By construction,
![]() $ \eta_2 $
respects the two face maps
$ \eta_2 $
respects the two face maps
![]() $ \delta^2_0 $
and
$ \delta^2_0 $
and
![]() $ \delta^2_2 $
, since these are just pullback projections. In addition,
$ \delta^2_2 $
, since these are just pullback projections. In addition,
![]() $ \eta_2 $
respects the two degeneracy maps since these are induced by
$ \eta_2 $
respects the two degeneracy maps since these are induced by
![]() $ {\mathrm{id}} $
above, and
$ {\mathrm{id}} $
above, and
![]() $ \eta_1 $
respects
$ \eta_1 $
respects
![]() $ {\mathrm{id}} $
. Finally, we need to check that
$ {\mathrm{id}} $
. Finally, we need to check that
![]() $ \eta_2 $
respects composition. But composition of R-module homomorphisms is defined by composing the underlying maps, and since we can check equality of R -module homomorphisms on the underlying maps, this follows from the corresponding statement for sets.
$ \eta_2 $
respects composition. But composition of R-module homomorphisms is defined by composing the underlying maps, and since we can check equality of R -module homomorphisms on the underlying maps, this follows from the corresponding statement for sets.
We conclude that
![]() $ \eta $
defines a natural equivalence of 2-restricted simplicial objects, as desired.
$ \eta $
defines a natural equivalence of 2-restricted simplicial objects, as desired.
Finally, we explain the semantics of Theorem 3.3.10 and Corollary 3.3.9 for module categories. To any object X in
![]() $ {\mathscr{X}} $
(more generally, any morphism), we have the usual sequence of adjoints
$ {\mathscr{X}} $
(more generally, any morphism), we have the usual sequence of adjoints
The right adjoints automatically lift to categories of modules, being left-exact. By the internal cocompleteness of categories of modules, we have a corresponding leftmost adjoint
![]() $ {\mathrm{colim}_{X}} $
. By Corollary 3.3.9,
$ {\mathrm{colim}_{X}} $
. By Corollary 3.3.9,
![]() $ {\mathrm{colim}_{X}} $
preserves internal products, and Theorem 3.3.10 implies that it is internally left-exact whenever X is 0-truncated. On global points, we deduce the following:
$ {\mathrm{colim}_{X}} $
preserves internal products, and Theorem 3.3.10 implies that it is internally left-exact whenever X is 0-truncated. On global points, we deduce the following:
Theorem 4.3.5 Let R be a ring object in
![]() $ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
, and let
$ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
, and let
![]() $ X \in {\mathscr{X}} $
. We have an adjunction:
$ X \in {\mathscr{X}} $
. We have an adjunction:
where
![]() $ {\mathrm{colim}_{X}} $
preserves finite products. If X is 0-truncated, then
$ {\mathrm{colim}_{X}} $
preserves finite products. If X is 0-truncated, then
![]() $ \bigoplus_X \equiv {\mathrm{colim}_{X}} $
is left-exact.
$ \bigoplus_X \equiv {\mathrm{colim}_{X}} $
is left-exact.
We emphasise that this is an external statement about ordinary categories, and left-exactness refers to preservation of finite limits in the usual (external) sense.
Proof. From Theorem 3.3.10, we get an adjunction between Rezk (1,1)-objects in
![]() ${\mathscr{X}}$
${\mathscr{X}}$
which yields an adjunction on global points. Using the previous theorem and that
![]() ${{\mathrm{\mathtt{const}}}_{X}}$
corresponds to base change on global points, we obtain the desired adjunction
${{\mathrm{\mathtt{const}}}_{X}}$
corresponds to base change on global points, we obtain the desired adjunction
![]() ${\mathrm{colim}_{X}} \dashv X \times (-)$
.
${\mathrm{colim}_{X}} \dashv X \times (-)$
.
We now argue that
![]() ${\mathrm{colim}_{X}}$
preserves finite products. For any (external) natural number n, the product of an n-element family
${\mathrm{colim}_{X}}$
preserves finite products. For any (external) natural number n, the product of an n-element family
![]() $ A : n \to {{(X{\times}R)}\textrm{-}{\mathrm{Mod}}} $
can be computed as the (internal) limit of the internalisation
$ A : n \to {{(X{\times}R)}\textrm{-}{\mathrm{Mod}}} $
can be computed as the (internal) limit of the internalisation
![]() $ \underline{A} : \ell_*(n) \to {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}^X $
, by Proposition 4.1.9. The object
$ \underline{A} : \ell_*(n) \to {{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}^X $
, by Proposition 4.1.9. The object
![]() $ \ell_*(n) $
is the standard n-element set in
$ \ell_*(n) $
is the standard n-element set in
![]() ${\mathscr{X}}$
, which is internally finite (indeed, equivalent to the object
${\mathscr{X}}$
, which is internally finite (indeed, equivalent to the object
![]() $ {{\mathrm{\mathtt{Fin}}}(n)} $
). Hence,
$ {{\mathrm{\mathtt{Fin}}}(n)} $
). Hence,
![]() $ {\mathrm{\mathtt{colim}}_{X}} $
preserves the (internal) limit of
$ {\mathrm{\mathtt{colim}}_{X}} $
preserves the (internal) limit of
![]() $ \underline{A} $
by Corollary 3.3.9. From this, we deduce a sequence of equivalences
$ \underline{A} $
by Corollary 3.3.9. From this, we deduce a sequence of equivalences
where the first and third equivalences use Proposition 4.1.9 for limits, and that
![]() ${\mathrm{colim}_{X}}$
is given by
${\mathrm{colim}_{X}}$
is given by
![]() ${\mathrm{\mathtt{colim}}_{X}}$
on global points (as shown at the beginning of this proof). Thus,
${\mathrm{\mathtt{colim}}_{X}}$
on global points (as shown at the beginning of this proof). Thus,
![]() ${\mathrm{colim}_{X}}$
preserves finite products.
${\mathrm{colim}_{X}}$
preserves finite products.
Now suppose that X is a set. To see that
![]() $ \bigoplus_X $
is left-exact it suffices to show that it preserves equalisers, since we already know that it preserves finite products. Applying
$ \bigoplus_X $
is left-exact it suffices to show that it preserves equalisers, since we already know that it preserves finite products. Applying
![]() $ \ell_* $
to an equaliser diagram in
$ \ell_* $
to an equaliser diagram in
![]() ${{(X{\times}R)}\textrm{-}{\mathrm{Mod}}}$
produces an internal equaliser diagram in
${{(X{\times}R)}\textrm{-}{\mathrm{Mod}}}$
produces an internal equaliser diagram in
![]() ${{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}^X$
. The claim then follows by an argument similar to the one above, using that
${{R}{\textrm{-}}{\mathrm{\mathtt{Mod}}}}^X$
. The claim then follows by an argument similar to the one above, using that
![]() ${\mathrm{\mathtt{colim}}_{X}}$
respects internal equalisers when X is a set by Theorem 3.3.10.
${\mathrm{\mathtt{colim}}_{X}}$
respects internal equalisers when X is a set by Theorem 3.3.10.
We end by discussing the relation of this theorem to Harting (Reference Harting1982, Theorem 2.7).
Remark 4.3.6 Harting’s construction of the left-exact coproduct applies to any elementary 1-topos with
![]() ${\mathbb{N}}$
. The 1-topos
${\mathbb{N}}$
. The 1-topos
![]() $ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
is, in particular, an elementary topos, hence Theorem 2.7 of loc. cit. implies the 0-truncated and
$ {\tau_{\leq 0}({{\mathscr{X}_{\kappa}}})} $
is, in particular, an elementary topos, hence Theorem 2.7 of loc. cit. implies the 0-truncated and
![]() $ R \equiv {\mathbb{Z}} $
case of our theorem above. (The case for general R is covered by Blechschmidt 2018, Proposition 3.7 for modules.) Conversely, a Grothendieck 1-topos
$ R \equiv {\mathbb{Z}} $
case of our theorem above. (The case for general R is covered by Blechschmidt 2018, Proposition 3.7 for modules.) Conversely, a Grothendieck 1-topos
![]() $ \mathrm{Sh}_0({\mathscr{C}}) $
is equivalent to the 0-truncated fragment of the
$ \mathrm{Sh}_0({\mathscr{C}}) $
is equivalent to the 0-truncated fragment of the
![]() $\infty$
-topos
$\infty$
-topos
![]() $ \mathrm{Sh}_\infty ({\mathscr{C}}) $
of
$ \mathrm{Sh}_\infty ({\mathscr{C}}) $
of
![]() $\infty$
-sheaves on the same site (see Proposition 4.2.4). Consequently, we recover Harting’s theorem for
$\infty$
-sheaves on the same site (see Proposition 4.2.4). Consequently, we recover Harting’s theorem for
![]() $ \mathrm{Sh}_0({\mathscr{C}}) $
by applying our theorem to
$ \mathrm{Sh}_0({\mathscr{C}}) $
by applying our theorem to
![]() $ \mathrm{Sh}_\infty ({\mathscr{C}}) $
.
$ \mathrm{Sh}_\infty ({\mathscr{C}}) $
.
Though there is a proposal (Cherradi, Reference Cherradi2022) for interpreting HoTT into any elementary
![]() $\infty$
-topos (Rasekh, Reference Rasekh2022), we do now know whether any elementary 1-topos can be realised as the 0-truncated fragment of the latter. However, if this is the case, then our Theorem 4.3.5 would imply Harting’s theorem in the elementary setting as well.
$\infty$
-topos (Rasekh, Reference Rasekh2022), we do now know whether any elementary 1-topos can be realised as the 0-truncated fragment of the latter. However, if this is the case, then our Theorem 4.3.5 would imply Harting’s theorem in the elementary setting as well.
InHarting (Reference Harting1982), the construction of the internal coproduct of abelian groups occupies almost 60 pages. The length was largely due to the underdeveloped state of the internal language of an elementary 1-topos at the time. However, once the construction was complete, left-exactness followed by general results in Johnstone (Reference Johnstone1977). By contrast, our generalised construction is essentially contained in Section 3.3, which weighs in at just over 2 pages. The analogues of the general results of Johnstone (Reference Johnstone1977) in our setting (or at least the parts we needed) are embodied by Proposition 4.1.9 and the theory about filtered colimits that we developed in Section 2.3.
Acknowledgements
I am grateful to both Nima Rasekh and Raffael Stenzel for helpful discussions about universes and representability and to my adviser Dan Christensen for countless suggestions which have helped improve this text. I would also like to thank the anonymous referees for valuable comments. We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), RGPIN-2022-04739.