Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T17:16:15.371Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST-PRIME VALUES OF BINARY FORMS WITH ONE PRIME VARIABLE

Part of: Multiplicative number theory

Published online by Cambridge University Press:  05 December 2014

A. J. Irving
A. J. Irving*
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, U.K. email irving@maths.ox.ac.uk
Get access

Abstract

By establishing an improved level of distribution we study almost-primes of the form $f(p,n)$ where 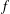$f$ is an irreducible binary form over 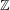$\mathbb{Z}$.

MSC classification

Primary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 61 , Issue 3 , September 2015 , pp. 741 - 755
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Daniel, S., On the divisor-sum problem for binary forms. J. Reine Angew. Math. 507 1999, 107–129.CrossRefGoogle Scholar
Fouvry, E. and Iwaniec, H., Gaussian primes. Acta Arith. 79(3) 1997, 249–287.CrossRefGoogle Scholar
Greaves, G., Large prime factors of binary forms. J. Number Theory 3 1971, 35–59.CrossRefGoogle Scholar
Greaves, G., Sieves in Number Theory (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)] 43), Springer (Berlin, 2001).CrossRefGoogle Scholar
Heath-Brown, D. R., Primes represented by x 3 + 2y 3. Acta Math. 186(1) 2001, 1–84.CrossRefGoogle Scholar
Montgomery, H. L., Maximal variants of the large sieve. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28(3) 1982, 805–812 (1981).Google Scholar
Richert, H.-E., Selberg’s sieve with weights. Mathematika 16 1969, 1–22.CrossRefGoogle Scholar