Article contents
ARRANGEMENTS OF HOMOTHETS OF A CONVEX BODY
Published online by Cambridge University Press: 09 August 2017
Abstract
Answering a question of Füredi and Loeb [On the best constant for the Besicovitch covering theorem. Proc. Amer. Math. Soc.121(4) (1994), 1063–1073], we show that the maximum number of pairwise intersecting homothets of a 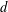 $d$ -dimensional centrally symmetric convex body
$d$ -dimensional centrally symmetric convex body 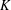 $K$ , none of which contains the center of another in its interior, is at most
$K$ , none of which contains the center of another in its interior, is at most 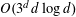 $O(3^{d}d\log d)$ . If
$O(3^{d}d\log d)$ . If 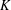 $K$ is not necessarily centrally symmetric and the role of its center is played by its centroid, then the above bound can be replaced by
$K$ is not necessarily centrally symmetric and the role of its center is played by its centroid, then the above bound can be replaced by 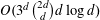 $O(3^{d}\binom{2d}{d}d\log d)$ . We establish analogous results for the case where the center is defined as an arbitrary point in the interior of
$O(3^{d}\binom{2d}{d}d\log d)$ . We establish analogous results for the case where the center is defined as an arbitrary point in the interior of 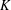 $K$ . We also show that, in the latter case, one can always find families of at least
$K$ . We also show that, in the latter case, one can always find families of at least 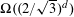 $\unicode[STIX]{x1D6FA}((2/\sqrt{3})^{d})$ translates of
$\unicode[STIX]{x1D6FA}((2/\sqrt{3})^{d})$ translates of 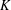 $K$ with the above property.
$K$ with the above property.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2017
References
- 8
- Cited by

