Article contents
A CODING OF BUNDLE GRAPHS AND THEIR EMBEDDINGS INTO BANACH SPACES
Published online by Cambridge University Press: 06 August 2018
Abstract
The purpose of this article is to generalize some known characterizations of Banach space properties in terms of graph preclusion. In particular, it is shown that superreflexivity can be characterized by the non-equi-bi-Lipschitz embeddability of any family of bundle graphs generated by a non-trivial finitely branching bundle graph. It is likewise shown that asymptotic uniform convexifiability can be characterized within the class of reflexive Banach spaces with an unconditional asymptotic structure by the non-equi-bi-Lipschitz embeddability of any family of bundle graphs generated by a non-trivial 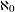 $\aleph _{0}$-branching bundle graph. For the specific case of
$\aleph _{0}$-branching bundle graph. For the specific case of 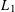 $L_{1}$, it is shown that every countably branching bundle graph bi-Lipschitzly embeds into
$L_{1}$, it is shown that every countably branching bundle graph bi-Lipschitzly embeds into 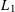 $L_{1}$ with distortion no worse than
$L_{1}$ with distortion no worse than 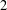 $2$.
$2$.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
References
- 5
- Cited by

