Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-11T01:34:38.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Dense sequences of convex polytopes

Published online by Cambridge University Press:  26 February 2010

M. A. Perles  and
G. C. Shephard
M. A. Perles
Affiliation:
Hebrew University of Jerusalem, Israel, andUniversity of East Anglia, Norwich, England.
G. C. Shephard
Affiliation:
Hebrew University of Jerusalem, Israel, andUniversity of East Anglia, Norwich, England.
Get access

Extract

Let P be a d-dimensional convex polytope (briefly, a d-polytope) in d-dimensional euclidean space Ed. Associated with P is a vector f(P), known as the f-vector of P, defined by

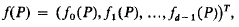
where fj(P) is the number of j-faces of P for 0 ≤ j ≤ d − 1 and the superscript T denotes transposition. (We regard f(P) as a column vector, and identify it with the vector

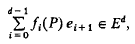
where (e1, …, ed) is some fixed basis of Ed.) Let 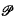d be the set of all d-polytopes in Ed, and 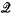d be any subset of 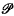d. Using tghe notation of [1; §8.1], we donate by f(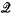d) the set of vectors {f(P): P ε 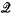d}, and write aff f(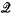d) for the (unique) affine subspace of lowest dimension in Ed which contains all the vectors of f(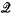d). Then it is well-known that

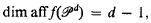
the equation of the hyperplane aff f(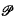d) being that given by the Euler relation between the numbers fj(P) [1; Theorem 8.1.1].

Type
Research Article
Information
Mathematika , Volume 17 , Issue 1 , June 1970 , pp. 28 - 38
Copyright
Copyright © University College London 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Grünbaum, B., Convex polytopes, (London–New York–Sydney, 1967).Google Scholar
2.Perles, M. A. and Shephard, G. C., “Facets and nonfacets of convex polytopes”, Acta Math., 119 (1967), 113–145.CrossRefGoogle Scholar
3.Shephard, G. C., “Approximations by polytopes with projectively regular facets”, Mathematika, 13 (1966), 189–195.CrossRefGoogle Scholar