Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Wen-Ch'ing Winnie
and
Moroz, B.Z
1985.
On ideal classes of number fields containing integral ideals of equal norms.
Journal of Number Theory,
Vol. 21,
Issue. 2,
p.
185.
Coleman, M.D
1992.
The distribution of points at which norm-forms are prime.
Journal of Number Theory,
Vol. 41,
Issue. 3,
p.
359.
Coleman, M. D.
1998.
The normal density of prime ideals in small regions.
Monatshefte f�r Mathematik,
Vol. 125,
Issue. 2,
p.
111.
Coleman, Mark D.
2001.
The Hooley-Huxley contour method for problems in number fields III : frobenian functions.
Journal de théorie des nombres de Bordeaux,
Vol. 13,
Issue. 1,
p.
65.

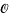 denote the ring of integers of
denote the ring of integers of