Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T04:29:10.031Z Has data issue: false hasContentIssue false
  • English
  • Français

ENVELOPES FOR SETS AND FUNCTIONS: REGULARIZATION AND GENERALIZED CONJUGACY

Part of: Existence theories General convexity Approximations and expansions

Published online by Cambridge University Press:  23 February 2017

A. Cabot ,
A. Jourani  and
L. Thibault
A. Cabot
Affiliation:
Institut de Mathématiques de Bourgogne, UMR 5584, CNRS, Université Bourgogne Franche-Comté, 21000 Dijon, France email alexandre.cabot@u-bourgogne.fr
A. Jourani
Affiliation:
Institut de Mathématiques de Bourgogne, UMR 5584, CNRS, Université Bourgogne Franche-Comté, 21000 Dijon, France email abderrahim.jourani@u-bourgogne.fr
L. Thibault
Affiliation:
Institut Montpelliérain Alexander Grothendieck, Université de Montpellier, Place EugÚne Bataillon, 34095 Montpellier, France Centro de Modelamiento MatematicoUniversidad de Chile, Chile email lionel.thibault@univ-montp2.fr
Get access

Abstract

Let 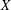$X$ be a vector space and let 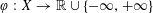$\unicode[STIX]{x1D711}:X\rightarrow \mathbb{R}\cup \{-\infty ,+\infty \}$ be an extended real-valued function. For every function 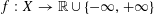$f:X\rightarrow \mathbb{R}\cup \{-\infty ,+\infty \}$, let us define the 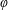$\unicode[STIX]{x1D711}$-envelope of 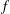$f$ by

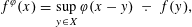$$\begin{eqnarray}f^{\unicode[STIX]{x1D711}}(x)=\sup _{y\in X}\unicode[STIX]{x1D711}(x-y)\begin{array}{@{}c@{}}-\\ \cdot \end{array}f(y),\end{eqnarray}$$
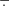where $\begin{array}{@{}c@{}}-\\ \\ \\ \cdot \end{array}$ denotes the lower subtraction in 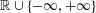$\mathbb{R}\cup \{-\infty ,+\infty \}$. The main purpose of this paper is to study in great detail the properties of the important generalized conjugation map 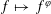$f\mapsto f^{\unicode[STIX]{x1D711}}$. When the function 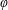$\unicode[STIX]{x1D711}$ is closed and convex, 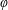$\unicode[STIX]{x1D711}$-envelopes can be expressed as Legendre–Fenchel conjugates. By particularizing with 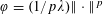$\unicode[STIX]{x1D711}=(1/p\unicode[STIX]{x1D706})\Vert \cdot \Vert ^{p}$, for 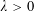$\unicode[STIX]{x1D706}>0$ and 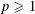$p\geqslant 1$, this allows us to derive new expressions of the Klee envelopes with index 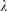$\unicode[STIX]{x1D706}$ and power 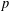$p$. Links between 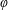$\unicode[STIX]{x1D711}$-envelopes and Legendre–Fenchel conjugates are also explored when 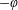$-\unicode[STIX]{x1D711}$ is closed and convex. The case of Moreau envelopes is examined as a particular case. In addition to the 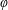$\unicode[STIX]{x1D711}$-envelopes of functions, a parallel notion of envelope is introduced for subsets of 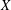$X$. Given subsets 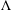$\unicode[STIX]{x1D6EC}$, 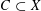$C\subset X$, we define the 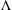$\unicode[STIX]{x1D6EC}$-envelope of 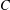$C$ as 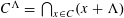$C^{\unicode[STIX]{x1D6EC}}=\bigcap _{x\in C}(x+\unicode[STIX]{x1D6EC})$. Connections between the transform 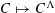$C\mapsto C^{\unicode[STIX]{x1D6EC}}$ and the aforestated 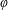$\unicode[STIX]{x1D711}$-conjugation are investigated.

MSC classification

Primary: 52A41: Convex functions and convex programs 49J53: Set-valued and variational analysis 41A65: Abstract approximation theory (approximation in normed linear spaces and other abstract spaces)
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 383 - 432
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Attouch, H., Buttazzo, G. and Michaille, G., Variational analysis in Sobolev and BV spaces. In Applications to PDE’s and Optimization (MPS/SIAM Series on Optimization 6 ), Society for Industrial and Applied Mathematics (SIAM) (Philadelphia, PA, 2006).Google Scholar
Auslender, A. and Teboulle, M., Asymptotic Cones and Functions in Optimization and Variational Inequalities (Springer Monographs in Mathematics), Springer (New York, 2003).Google Scholar
Aze, D. and Volle, M., Various continuity properties of the deconvolution. In Advances in Optimization (Lectures Notes in Economics and Mathematical Systems 382 ), Springer (1992), 16–30.Google Scholar
Balder, E. J., An extension of duality-stability relations to nonconvex optimization problems. SIAM J. Control Optim. 15 1977, 329–343.CrossRefGoogle Scholar
Brþnsted, A. and Rockafellar, R. T., On the subdifferentiability of convex functions. Proc. Amer. Math. Soc. 16 1965, 605–611.CrossRefGoogle Scholar
Dolecki, S., Polarities and generalized extremal convolutions. J. Convex Anal. 23 2016, 603–614.Google Scholar
Dolecki, S. and Kurcyusz, S., On đ›·-convexity in extremal problems. SIAM J. Control Optim. 16 1978, 277–300.Google Scholar
Ekeland, I. and Temam, R., Convex analysis and variational problems. In SIAM Classics in Applied Mathematics (EkeTem 28 ), Society for Industrial and Applied Mathematics (Philadelphia, PA, 1999).Google Scholar
Elster, K.-H. and Wolf, A., Recent results on generalized conjugate functions. In Trends in Mathematical Optimization, BirkhĂ€user (Basel, 1988), 67–78.CrossRefGoogle Scholar
Granero, A. S., JimĂ©nez-Sevilla, M. and Moreno, J. P., Intersections of closed balls and geometry of Banach spaces. Extracta Math. 19(1) 2004, 55–92.Google Scholar
Hiriart-Urruty, J.-B., A general formula on the conjugate of the difference of functions. Canad. Math. Bull. 29 1986, 482–485.CrossRefGoogle Scholar
Hiriart-Urruty, J.-B., The deconvolution operation in convex analysis: an introduction. Cybernet. Systems Anal. 30 1994, 555–560.CrossRefGoogle Scholar
Hiriart-Urruty, J.-B. and Lemaréchal, C., Convex analysis and minimization algorithms, I. Fundamentals, II. In Advanced Theory and Bundle Methods, Springer (Berlin, 1993).Google Scholar
Hiriart-Urruty, J.-B. and Mazure, M.-L., Formulations variationnelles de l’addition parallĂšle et de la soustraction parallĂšlle d’opĂ©rateurs semi-dĂ©finis positifs. C. R. Acad. Sci. Paris, SĂ©r. I 302 1986, 527–530.Google Scholar
Ivanov, G. E., Weak convexity of functions and the infimal convolution. J. Convex Anal. 23 2016, 719–732.Google Scholar
Jourani, A., Thibault, L. and Zagrodny, D., The NSLUC property and Klee envelope. Math. Ann. 365(3–4) 2016, 923–967.Google Scholar
Martinez-Legaz, J.-E., Generalized conjugation and related topics. In ‘Generalized Convexity and Fractional Programming with Economic Applications’, Proc. Pisa. Italy (1988) (Lecture Notes in Economics and Mathematical Systems 345 ) (ed. Cambini, A. et al. ), Springer (Berlin, 1990), 168–197.Google Scholar
Martinez-Legaz, J.-E. and Penot, J.-P., Regularization by erasement. Math. Scand. 98 2006, 97–124.CrossRefGoogle Scholar
Mazur, S., Über schwache Konvergentz in den Raumen L p . Studia Math. 4 1933, 128–133.Google Scholar
Moreau, J. J., ProximitĂ© et dualitĂ© dans un espace hilbertien. Bull. Soc. Math. France 93 1965, 273–299.Google Scholar
Moreau, J. J., Inf-convolution, sous-additivitĂ©, convexitĂ© des fonctions numĂ©riques. J. Math. Pures Appl. 49 1970, 109–154.Google Scholar
Moreau, J. J., Fonctionnelles convexes. In Collùge de France, Paris (1967), 2nd edn., Consiglio Nazionale delle Ricerche and Facoltá di Ingegneria Universita di Roma ‘Tor Vergata’ (2003).Google Scholar
Penot, J.-P., Calculus Without Derivatives (Graduate Texts in Mathematics), Springer (New York, 2013).CrossRefGoogle Scholar
Penot, J.-P. and Volle, M., On strongly convex and paraconvex dualities. In ‘Generalized Convexity and Fractional Programming with Economic Applications’, Proc. Pisa. Italy (1988) (Lecture Notes in Economics and Mathematical Systems 345 ) (ed. Cambini, A. et al. ), Springer (Berlin, 1990), 198–218.Google Scholar
Polovinkin, E. S., On strongly convex sets and strongly convex functions. J. Math. Sci. 100 2000, 2633–2681.Google Scholar
Polovinkin, E. S. and Balashov, M. V., Elements of Convex and Strongly Convex Analysis, Fizmatlit (Moscow, 2004) (Russian).Google Scholar
Pshenichnyi, B. N., Leçons sur les jeux diffĂ©rentiels. Cah. l’I.R.I.A.(4) 1971, 145–226.Google Scholar
Rockafellar, R. T., Convex Analysis, Princeton University Press (Princeton, NJ, 1970).Google Scholar
Rockafellar, R. T., Augmented Lagrange multipliers functions and duality in nonconvex programming. SIAM J. Control Optim. 12 1974, 268–285.Google Scholar
Rockafellar, R. T. and Wets, R. J.-B., Variational Analysis, Springer (Berlin, 1998).CrossRefGoogle Scholar
Rubinov, A., Abstract Convexity and Global Optimization, Kluwer (Dordrecht, 2000).CrossRefGoogle Scholar
Singer, I., Conjugation operators. In Selected Topics in Operations Research and Mathematical Economics (eds Hammer, G. and Pallaschke, D.), Springer (Berlin, 1984), 80–97.CrossRefGoogle Scholar
Singer, I., Some Relations between Dualities, Polarities, Coupling Functionals, and Conjugations. J. Math. Anal. Appl. 115 1986, 1–22.CrossRefGoogle Scholar
Singer, I., Duality for Nonconvex Approximation and Optimization (CMS Books in Mathematics), Springer (New York, 2006).CrossRefGoogle Scholar
Vesely, L., Affine mappings and convex functions. Examples of convex functions. Preprint, available at http://www.mat.unimi.it/users/libor/AnConvessa/functions.pdf.Google Scholar
Vial, J.-P., Strong and weak convexity of sets and functions. Math. Oper. Res. 8 1983, 231–259.Google Scholar
Volle, M., Contributions Ă  la DualitĂ© et Ă  l’Épiconvergence. ThĂšse de Doctorat d’État, UniversitĂ© de Pau et des Pays de l’Adour, 1986.Google Scholar
Volle, M., A formula on the subdifferential of the deconvolution of convex functions. Bull. Aust. Math. Soc. 47 1993, 333–340.Google Scholar
Wang, X., On Chebyshev functions and Klee functions. J. Math. Anal. Appl. 368 2010, 293–310.CrossRefGoogle Scholar