Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dickinson, H.
Dodson, M.M.
and
Yuan, J.
1999.
Hausdorff dimension and p-adic diophantine approximation.
Indagationes Mathematicae,
Vol. 10,
Issue. 3,
p.
337.
Dodson, Maurice
2002.
Rigidity in Dynamics and Geometry.
p.
77.
Kemble, R. S.
2005.
A Groshev Theorem for Small Linear Forms.
Mathematika,
Vol. 52,
Issue. 1-2,
p.
79.
HUSSAIN, MUMTAZ
2011.
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS.
Bulletin of the Australian Mathematical Society,
Vol. 83,
Issue. 2,
p.
262.
DICKINSON, DETTA
and
HUSSAIN, MUMTAZ
2013.
THE METRIC THEORY OF MIXED TYPE LINEAR FORMS.
International Journal of Number Theory,
Vol. 09,
Issue. 01,
p.
77.
HUSSAIN, M.
and
KRISTENSEN, S.
2013.
METRICAL RESULTS ON SYSTEMS OF SMALL LINEAR FORMS.
International Journal of Number Theory,
Vol. 09,
Issue. 03,
p.
769.
Hussain, Mumtaz
and
Levesley, Jason
2013.
The metrical theory of simultaneously small linear forms.
Functiones et Approximatio Commentarii Mathematici,
Vol. 48,
Issue. 2,
Steinerberger, Stefan
2016.
Directional Poincaré inequalities along mixing flows.
Arkiv för Matematik,
Vol. 54,
Issue. 2,
p.
555.
Allen, Demi
and
Beresnevich, Victor
2018.
A mass transference principle for systems of linear forms and its applications.
Compositio Mathematica,
Vol. 154,
Issue. 5,
p.
1014.
Hussain, Mumtaz
Kristensen, Simon
and
Simmons, David
2020.
Metrical theorems on systems of affine forms.
Journal of Number Theory,
Vol. 213,
Issue. ,
p.
67.

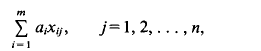

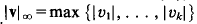 of any vector in
of any vector in 