Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-11T01:23:48.804Z Has data issue: false hasContentIssue false
  • English
  • Français

On discrepancy bounds via dual shatter function

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  26 February 2010

Jiří Matousěk
Jiří Matousěk
Affiliation:
Department of Applied Mathematics, Charles University, Malostranské nám. 25, 118 00 Praha 1, Czech Republic
Get access

Abstract

Recently, it has been shown that tight or almost tight upper bounds for the discrepancy of many geometrically denned set systems can be derived from simple combinatorial parameters of these set systems. Namely, if the primal shatter function of a set system ℛ on an n-point set X is bounded by const. md, then the discrepancy disc (ℛ) = O(n(d−1)/2d) (which is known to be tight), and if the dual shatter function is bounded by const. md, then disc 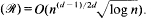We prove that for d = 2, 3, the latter bound also cannot be improved in general. We also show that bounds on the shatter functions alone do not imply the average (L1)-discrepancy to be much smaller than the maximum discrepancy: this contrasts results of Beck and Chen for certain geometric cases. In the proof we give a construction of a certain asymptotically extremal bipartite graph, which may be of independent interest.

MSC classification

Secondary: 11K41: Continuous, $p$-adic and abstract analogues
Type
Research Article
Information
Mathematika , Volume 44 , Issue 1 , June 1997 , pp. 42 - 49
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alexander, R.. Geometric methods in the study of irregularities of distribution. Combinatorica, 10 (1990), 115–136.CrossRefGoogle Scholar
2.Alon, N. and Spencer, J.. The Probabilistic Method (J. Wiley & Sons, 1993).Google Scholar
3.Beck, J.. Some upper bounds in the theory of irregularities of distribution. Acta Arith., 43 (1984), 115–130.CrossRefGoogle Scholar
4.Beck, J. and Chen, W.. Irregularities of Distribution (Cambridge University Press, 1987).CrossRefGoogle Scholar
5.Beck, J. and Chen, W.. Irregularities of point distribution relative to half-planes I. Mathematika, 40 (1993), 102–126.CrossRefGoogle Scholar
6.Beck, J. and Chen, W.. Irregularities of point distribution relative to convex polygons II. Mathematika, 40 (1993), 127–136.CrossRefGoogle Scholar
7.Beck, J. and Sós, V.. Discrepancy theory. In Handbook of Combinatorics, (North-Holland, Amsterdam, 1995), pp. 1405–1446.Google Scholar
8.Bollobás, B.. Extremal Graph Theory (Academic Press, London, 1978).Google Scholar
9.Brown, W. G.. On graphs that do not contain a Thomsen graph. Canad. Math. Bull., 9 (1966), 281–285.CrossRefGoogle Scholar
10.Harris, J.. Algebraic Geometry (Springer-Verlag, 1992).CrossRefGoogle Scholar
11.Kollar, J., Rónyai, L., and Szabó, T.. Norm-graphs and bipartite Turán numbers. Combinatorica, 16, (1996), 399–406.CrossRefGoogle Scholar
12.Matoušek, J.. Tight upper bounds for the discrepancy of halfspaces. Discr. & Comput. Geom., 13 (1995), 593–601.CrossRefGoogle Scholar
13.Matoušek, J., Welzl, E. and Wernisch, L.. Discrepancy and εapproximations for bounded VC-dimension. Combinatorica, 13 (1993), 455–466.CrossRefGoogle Scholar