Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
159.
Brüdern, Jörg
and
Wooley, Trevor D.
2017.
Additive representation in short intervals, II: sums of two like powers.
Mathematische Zeitschrift,
Vol. 286,
Issue. 1-2,
p.
179.
Kaneko, Hajime
2019.
Arithmetical properties of real numbers related to beta-expansions.
Functiones et Approximatio Commentarii Mathematici,
Vol. 60,
Issue. 2,
Ghidelli, Luca
2020.
Arbitrarily long gaps between the values of positive‐definite cubic and biquadratic diagonal forms.
Journal of the London Mathematical Society,
Vol. 102,
Issue. 1,
p.
43.


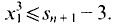 Then
Then 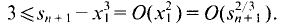 This procedure is iterated by choosing
This procedure is iterated by choosing 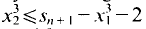 and
and 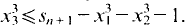 Thus
Thus 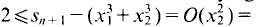
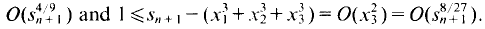 Since
Since 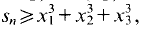 this implies (1).
this implies (1).