Article contents
On Integer Sets Containing Strings of Consecutive Integers
Published online by Cambridge University Press: 26 February 2010
Extract
By a well-known theorem of Szemerdi 8 any set of integers that has positive density contains arithmetic progressions of arbitrary length. One might expect that there are conditions of similar generality, under which an integer set contains arbitrarily long strings of consecutive integers, i.e., arithmetic progressions with 1 as common difference. Results of this kind would be of great importance because of potential applications to arithmetically interesting sets such as the set n: (n) = 1, where (n) is the Liouville function, or the sets
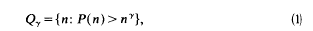
where P(n) denotes the greatest prime factor of n and 0<< 1. One naturally expects that such sets contain arbitrarily long strings of consecutive integers, but no results in this direction are known, and the problem seems to be a very difficult one, perhaps comparable in depth to the prime k-tuple conjecture.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright University College London 1989
References
- 6
- Cited by

