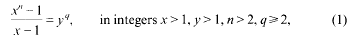Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shorey, T. N.
2000.
Number Theory.
p.
463.
Bugeaud, Yann
Mignotte, Maurice
and
Roy, Yves
2000.
On the Diophantine equation (xn- 1)/(x-1) = yq.
Pacific Journal of Mathematics,
Vol. 193,
Issue. 2,
p.
257.
Bugeaud, Yann
Cao, Zhenfu
and
Mignotte, Maurice
2001.
On Simple K4-Groups.
Journal of Algebra,
Vol. 241,
Issue. 2,
p.
658.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
209.
Bugeaud, Yann
Luca, Florian
Mignotte, Maurice
and
Siksek, Samir
2007.
Perfect powers from products of terms in Lucas sequences.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2007,
Issue. 611,
Luca, Florian
and
Szalay, Laszlo
2007.
Fibonacci numbers of the form
p
a
±
p
b
+ 1
.
The Fibonacci Quarterly,
Vol. 45,
Issue. 2,
p.
98.
AKHLAGHI, Z.
KHOSRAVI, B.
and
KHATAMI, M.
2010.
CHARACTERIZATION BY PRIME GRAPH OF PGL(2, pk) WHERE p AND k > 1 ARE ODD.
International Journal of Algebra and Computation,
Vol. 20,
Issue. 07,
p.
847.
Luca, Florian
and
Pollack, Paul
2011.
Multiperfect numbers with identical digits.
Journal of Number Theory,
Vol. 131,
Issue. 2,
p.
260.
Pollack, Paul
2011.
Perfect Numbers with Identical Digits.
Integers,
Vol. 11,
Issue. 4,
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
275.
Gómez Ruiz, Carlos Alexis
and
Luca, Florian
2017.
Multiplicative Diophantine equations with factors from different Lucas sequences.
Journal of Number Theory,
Vol. 170,
Issue. ,
p.
282.
Bridy, Andrew
Oliver, Robert J. Lemke
Shallit, Arlo
and
Shallit, Jeffrey
2019.
The Generalized Nagell–Ljunggren Problem: Powers with Repetitive Representations.
Experimental Mathematics,
Vol. 28,
Issue. 4,
p.
428.
Adegbindin, Chèfiath
Luca, Florian
and
Togbé, Alain
2019.
Lucas numbers as sums of two repdigits.
Lithuanian Mathematical Journal,
Vol. 59,
Issue. 3,
p.
295.
Dujella, Andrej
Jukić Bokun, Mirela
and
Soldo, Ivan
2019.
A Pellian Equation with Primes and Applications to
$$D(-1)$$
D
(
-
1
)
-Quadruples.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 42,
Issue. 5,
p.
2915.
Gómez, Carlos A.
Luca, Florian
and
Zottor, Faith Shadow
2020.
On X-coordinates of Pell equations which are repdigits.
Research in Number Theory,
Vol. 6,
Issue. 4,
Adegbindin, Chèfiath
Luca, Florian
and
Togbé, Alain
2020.
Pell and Pell–Lucas Numbers as Sums of Two Repdigits.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 2,
p.
1253.
Alahmadi, Adel
Altassan, Alaa
Luca, Florian
and
Shoaib, Hatoon
2021.
Fibonacci numbers which are concatenations of two repdigits.
Quaestiones Mathematicae,
Vol. 44,
Issue. 2,
p.
281.
Alahmadi, Adel
Altassan, Alaa
Luca, Florian
and
Shoaib, Hatoon
2021.
k-generalized Fibonacci numbers which are concatenations of two repdigits.
Glasnik Matematicki,
Vol. 56,
Issue. 1,
p.
29.
Zhou, Yuetong
Yang, Peng
Zhang, Shaonan
and
Zhang, Kaiqiang
2022.
Repdigits as Sums of Four Tribonacci Numbers.
Symmetry,
Vol. 14,
Issue. 9,
p.
1931.
HASANALIZADE, ELCHIN
2023.
ON NEAR-PERFECT NUMBERS OF SPECIAL FORMS.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 3,
p.
366.