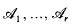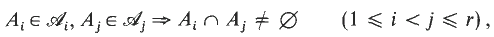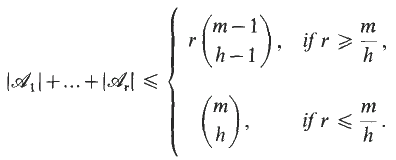Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
Chung, F.R.K
Graham, R.L
Frankl, P
and
Shearer, J.B
1986.
Some intersection theorems for ordered sets and graphs.
Journal of Combinatorial Theory, Series A,
Vol. 43,
Issue. 1,
p.
23.
1989.
Hypergraphs - Combinatorics of Finite Sets.
Vol. 45,
Issue. ,
p.
237.
Goldwasser, John
Hilton, Anthony J.W.
and
Zheng, Jie
2019.
Several families with incomparability and complementarity conditions.
Discrete Applied Mathematics,
Vol. 266,
Issue. ,
p.
103.