Article contents
On the Euler characteristic of spherical polyhedra and the Euler relation
Published online by Cambridge University Press: 26 February 2010
Extract
Let En+1, for some integer n ≥ 0, be the (n + 1)-dimensional Euclidean space, and denote by Sn the standard n–sphere in En+1, 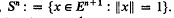 . It is convenient to introduce the (–1)-dimensional sphere
. It is convenient to introduce the (–1)-dimensional sphere 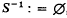 , where
, where  denotes the empty set. By an i-dimensional subsphere T of Sn, i = 0 n, we understand the intersection of Sn with some (i+1)-dimensional subspace of En+1. The affine hull of T always contains, with this definition, the origin of En+1.
denotes the empty set. By an i-dimensional subsphere T of Sn, i = 0 n, we understand the intersection of Sn with some (i+1)-dimensional subspace of En+1. The affine hull of T always contains, with this definition, the origin of En+1. 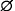 is the unique (–1)-dimensional subsphere of Sn. By the spherical hull, sph X, of a set
is the unique (–1)-dimensional subsphere of Sn. By the spherical hull, sph X, of a set 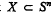 , we understand the intersection of all subspheres of Sn containing X. Further we set dim X: = dim sph X. The interior, the boundary and the complement of an arbitrary set
, we understand the intersection of all subspheres of Sn containing X. Further we set dim X: = dim sph X. The interior, the boundary and the complement of an arbitrary set 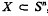 , with respect to Sn, shall be denoted by int X, bd X and cpl X. Finally we define the relative interior rel int X to be the interior of
, with respect to Sn, shall be denoted by int X, bd X and cpl X. Finally we define the relative interior rel int X to be the interior of 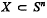 with respect to the usual topology sphZ
with respect to the usual topology sphZ 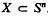 . For
. For 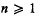 each (n–1)-dimensional subsphere of Sn defines two closed hemispheres of Sn, whose common boundary it is. The two hemispheres of the sphere Sº are denned to be the two one-pointed subsets of Sº. A subset
each (n–1)-dimensional subsphere of Sn defines two closed hemispheres of Sn, whose common boundary it is. The two hemispheres of the sphere Sº are denned to be the two one-pointed subsets of Sº. A subset 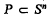 is called a closed (spherical) polytope, if it is the intersection of finitely many closed hemispheres, and, if, in addition, it does not contain a subsphere of Sn.
is called a closed (spherical) polytope, if it is the intersection of finitely many closed hemispheres, and, if, in addition, it does not contain a subsphere of Sn. 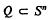 is called an i-dimensional, relatively open polytope,
is called an i-dimensional, relatively open polytope, 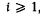 , or shortly an i-open polytope, if there exists a closed polytope
, or shortly an i-open polytope, if there exists a closed polytope 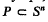 such that dim P = i and Q = rel int P.
such that dim P = i and Q = rel int P. 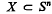 is called a closed polyhedron, if it is a finite union of closed polytopes P1 …, Pr. The empty set
is called a closed polyhedron, if it is a finite union of closed polytopes P1 …, Pr. The empty set 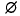 is the only (–1)-dimensional closed polyhedron of Sn. We denote by
is the only (–1)-dimensional closed polyhedron of Sn. We denote by 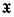 the set of all closed polyhedra of Sn.
the set of all closed polyhedra of Sn.  is called an i-open polyhedron, for some
is called an i-open polyhedron, for some  , if there are finitely many i-open polytopes Q1 …, Qr in Sn such that
, if there are finitely many i-open polytopes Q1 …, Qr in Sn such that 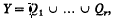 , and dim
, and dim 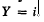 . By
. By 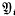 we denote the set of all i-open polyhedra. Clearly
we denote the set of all i-open polyhedra. Clearly 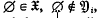 for all
for all 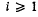 , and each i-dimensional subsphere of Sn,
, and each i-dimensional subsphere of Sn, 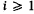 , belongs to
, belongs to 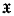 and to
and to 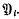 , For each i-dimensional subsphere T of Sn, set
, For each i-dimensional subsphere T of Sn, set 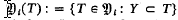 . A map
. A map 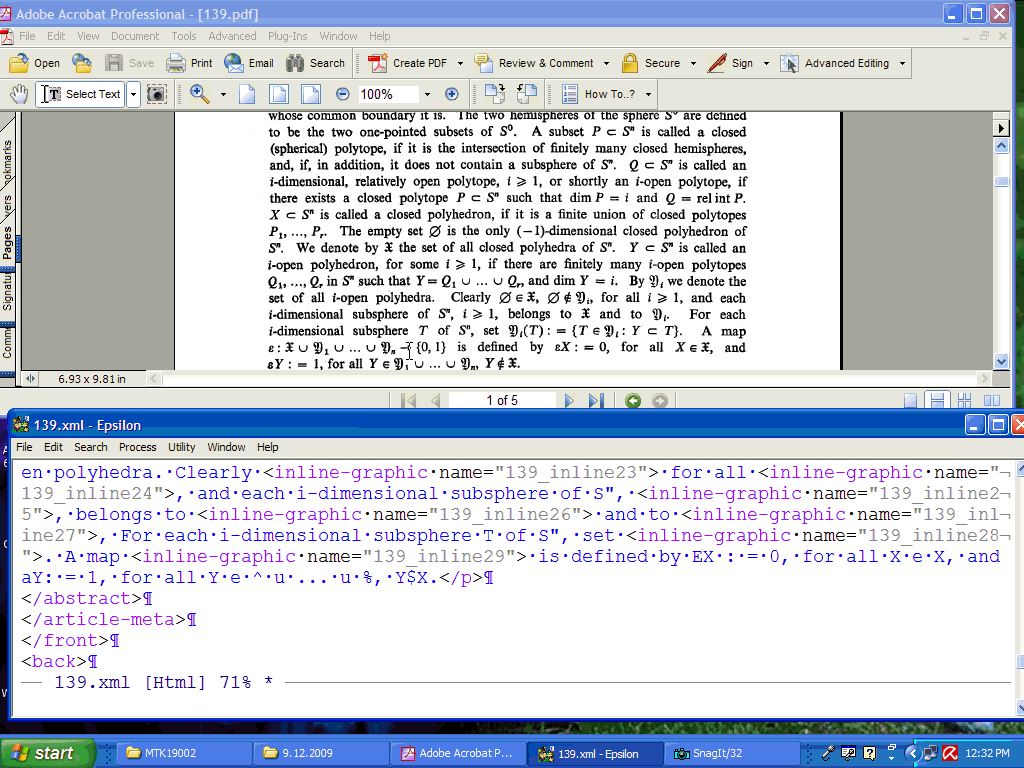 is defined by
is defined by 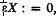 , for all
, for all 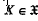 , and, for all
, and, for all 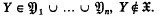 .
.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1972
References
- 9
- Cited by

