Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stoll, Michael
1992.
Galois groups over $$cQ$$ of some iterated polynomials.
Archiv der Mathematik,
Vol. 59,
Issue. 3,
p.
239.
Bridy, Andrew
and
Tucker, Thomas J.
2019.
Finite index theorems for iterated Galois groups of cubic polynomials.
Mathematische Annalen,
Vol. 373,
Issue. 1-2,
p.
37.
Li, Hua-Chieh
2020.
Arboreal Galois representation for a certain type of quadratic polynomials.
Archiv der Mathematik,
Vol. 114,
Issue. 3,
p.
265.
Li, Hua-Chieh
2021.
On Stoll’s criterion for the maximality of quadratic arboreal Galois representations.
Archiv der Mathematik,
Vol. 117,
Issue. 2,
p.
133.

 (a problem initially proposed by J. McKay). Setting
(a problem initially proposed by J. McKay). Setting  and Ω
and Ω ). Then Odoni proves that Ω
). Then Odoni proves that Ω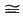 [C
[C