No CrossRef data available.
Article contents
Positive values of indefinite quadratic forms
Published online by Cambridge University Press: 26 February 2010
Extract
Let
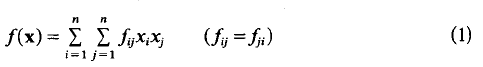
be a real quadratic form in n variables with integral coefficients (i.e., 2fij ε ℤ, fiiε ℤ.) and determinant D ≠ O. A well-known theorem of Cassels [1] states that if the equation f = 0 is properly soluble in integers x1 … , xn then there is a solution satisfying
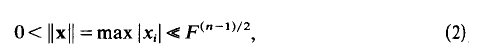
where F = max |fij and we use the «-notation with an implicit factor depending only on n. More recently it has been shown that f has n linearly independent zeros x1 …, xn satisfying
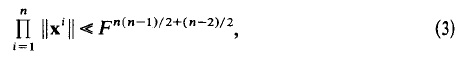
(see [2, 3 and 6])
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1986
References
1.Cassels, J. W. S.. Bounds for the least solutions of homogeneous quadratic equations. Proc. Camb. Phil Soc, 51 (1955), 262–264; Addendum, Proc. Camb. Phil Soc, 52 (1956), 604.CrossRefGoogle Scholar
2.Cook, R. J. and Raghavan, S.. Small independent zeros of quadratic forms. To appear.Google Scholar
3.Davenport, H.. Homogeneous quadratic equations. Mathematika, 18 (1971), 1–4.CrossRefGoogle Scholar
4.Lawton, B.. Bounded representations of the positive values of an indefinite quadratic form. Proc Camb. Phil. Soc, 54 (1958), 14–17.CrossRefGoogle Scholar
5.Mirsky, L.. Introduction to linear algebra (Oxford, 1955), reprinted by Paperbacks, Dover, New York, 1982.Google Scholar
6.Schulze-Pillot, R.. Small linearly independent zeros of quadratic forms. Monatsh. Math., 95 (1983), 241–249.CrossRefGoogle Scholar
7.Watson, G. L.. Least solutions of homogeneous quadratic equations. Proc. Camb. Phil. Soc, 53 (1957), 541–543.Google Scholar

