No CrossRef data available.
Article contents
RANDOM MULTIPLICATIVE WALKS ON THE RESIDUES MODULO  $n$
$n$
Published online by Cambridge University Press: 12 May 2017
Abstract
We introduce a new arithmetic function 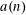 $a(n)$ defined to be the number of random multiplications by residues modulo
$a(n)$ defined to be the number of random multiplications by residues modulo  $n$ before the running product is congruent to zero modulo
$n$ before the running product is congruent to zero modulo  $n$ . We give several formulas for computing the values of this function and analyze its asymptotic behavior. We find that it is closely related to
$n$ . We give several formulas for computing the values of this function and analyze its asymptotic behavior. We find that it is closely related to 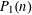 $P_{1}(n)$ , the largest prime divisor of
$P_{1}(n)$ , the largest prime divisor of  $n$ . In particular,
$n$ . In particular, 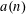 $a(n)$ and
$a(n)$ and 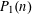 $P_{1}(n)$ have the same average order asymptotically. Furthermore, the difference between the functions
$P_{1}(n)$ have the same average order asymptotically. Furthermore, the difference between the functions 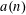 $a(n)$ and
$a(n)$ and 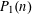 $P_{1}(n)$ is
$P_{1}(n)$ is 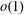 $o(1)$ as
$o(1)$ as  $n$ tends to infinity on a set with density approximately
$n$ tends to infinity on a set with density approximately 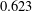 $0.623$ . On the other hand, however, we see that (except on a set of density zero) the difference between
$0.623$ . On the other hand, however, we see that (except on a set of density zero) the difference between 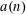 $a(n)$ and
$a(n)$ and 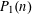 $P_{1}(n)$ tends to infinity on the integers outside this set. Finally, we consider the asymptotic behavior of the difference between these two functions and find that
$P_{1}(n)$ tends to infinity on the integers outside this set. Finally, we consider the asymptotic behavior of the difference between these two functions and find that 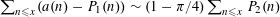 $\sum _{n\leqslant x}(a(n)-P_{1}(n))\sim (1-\unicode[STIX]{x1D70B}/4)\sum _{n\leqslant x}P_{2}(n)$ , where
$\sum _{n\leqslant x}(a(n)-P_{1}(n))\sim (1-\unicode[STIX]{x1D70B}/4)\sum _{n\leqslant x}P_{2}(n)$ , where 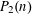 $P_{2}(n)$ is the second largest divisor of
$P_{2}(n)$ is the second largest divisor of  $n$ .
$n$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2017

