Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Spear, Donald W
1992.
Measures and self similarity.
Advances in Mathematics,
Vol. 91,
Issue. 2,
p.
143.
Bandt, Christoph
and
Haase, Hermann
1996.
Felix Hausdorff zum Gedächtnis.
p.
149.
Qu, Cheng Qin
Rao, Hui
and
Su, Wei Yi
2001.
Hausdorff Measure of Homogeneous Cantor Set.
Acta Mathematica Sinica, English Series,
Vol. 17,
Issue. 1,
p.
15.
Qu, Cheng-Qin
and
Zhou, Zuo-Ling
2006.
Hausdorff measures for a class of homogeneous Moran sets.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 65,
Issue. 2,
p.
442.
Baek, Hun-Ki
and
Lee, Hung-Hwan
2009.
Scaling Law of the Hausdorff Measure.
Kyungpook mathematical journal,
Vol. 49,
Issue. 4,
p.
619.
Qu, Cheng-qin
2013.
Hausdorff measures for a class of homogeneous cantor sets.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 29,
Issue. 1,
p.
117.
Yang, Ya-min
and
Zhang, Yuan
2021.
Lipschitz classification of Bedford-McMullen carpets with uniform horizontal fibers.
Journal of Mathematical Analysis and Applications,
Vol. 495,
Issue. 2,
p.
124742.
Attia, Najmeddine
and
Guizani, Omrane
2022.
A note on scaling properties of Hewitt Stromberg measure.
Filomat,
Vol. 36,
Issue. 10,
p.
3551.

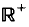 with θ(0)= 0 and let
with θ(0)= 0 and let 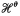 be the corresponding Hausdorff measure. We say that
be the corresponding Hausdorff measure. We say that 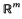 and
and