Hostname: page-component-76c49bb84f-bg8zk Total loading time: 0 Render date: 2025-07-10T07:49:32.892Z Has data issue: false hasContentIssue false
  • English
  • Français

Shadow-boundaries and cuts of convex polytopes

Published online by Cambridge University Press:  26 February 2010

Peter Kleinschmidt  and
Udo Pachner
Peter Kleinschmidt
Affiliation:
Institut för Mathematik, Ruhr-Universität Bochum, Bochum, West Germany
Udo Pachner
Affiliation:
Institut för Mathematik, Ruhr-Universität Bochum, Bochum, West Germany
Get access

Extract

Let P be a (convex) d-polytope in the Euclidean space Ed and p a point of Ed not contained in P or in a supporting hyperplane of a facet of P (we use the terminology of Grunbaum [2]). The part of the boundary of P which is “visible” from p, i.e. the union of those facets whose supporting hyperplanes separate p and P, form a (d – l)-ball, whose boundary is a (d – 2)-sphere S (all balls, spheres and manifolds to be considered are piecewise-linear). 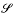The boundary-complex ℬ(P) induces a subdivision of S, which we call a (sharp) shadow-boundary ofP. 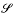is combinatorially isomorphic to the boundary complex of a poly tope which is a central projection of P from the point p on a hyperplane.

Information

Type
Research Article
Information
Mathematika , Volume 27 , Issue 1 , June 1980 , pp. 58 - 63
Copyright
Copyright © University College London 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Barnette, D. W.. “Projections of 3-polytopes”, Israel J. Math., 8 (1970), 304–308.CrossRefGoogle Scholar
2.Grönbaum, B.. Convex Polytopes (New York, Interscience, 1967).Google Scholar
3.Grönbaum, B.. “Arrangements and spreads”, Conference Board of the Math. Sciences Regional, Conf. Ser. in Math., No 10 (Amer. Math. Soc, 1972).Google Scholar
4.Kleinschmidt, P.. “Sphären mit wenigen Ecken”, Geom. Dedicata, 5 (1976), 307–320.CrossRefGoogle Scholar
5.Kleinschmidt, P.. “Stellare Abanderungen und Schalbarkeit von Komplexen und Polytopen”, Journ. of Geom., 11 (1978), 161–176.CrossRefGoogle Scholar
6.Pachner, U.. “Untersuchungen über Schnitte von kombinatorischen Mannigfaltigkeiten, insbesondere von Randkomplexen konvexer Polytope”, Dissertation (Bochum, 1975).Google Scholar
7.Pachner, U.. “Flache Einbettungen geschlossener Mannigfaltigkeiten der Kodimension 1 in Randkomplexe konvexer Polytope”, Math. Ann., 228 (1977), 187–196.CrossRefGoogle Scholar
8.Pachner, U.. “Baryzentrische Unterraumschnitte des Simplex”, Resultate der Math., 2 (1977), 105–110.CrossRefGoogle Scholar
9.Shephard, G. C.. “Sections and projections of convex polytopes”, Mathematika, 19 (1972), 144–162.CrossRefGoogle Scholar
10.Shephard, G. C.. “Subpolytopes of stack polytopes”, Israel J. Math., 19 (1974), 292–296.CrossRefGoogle Scholar