Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T23:01:26.270Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STEKLOV SPECTRUM OF CUBOIDS

Part of: Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  06 December 2018

Alexandre Girouard ,
Jean Lagacé ,
Iosif Polterovich  and
Alessandro Savo
Alexandre Girouard
Affiliation:
Département de mathématiques et de statistique, Pavillon Alexeandre-Vachon, Université Laval, Québec, QC G1V 0A6, Canada email alexandre.girouard@mat.ulaval.ca
Jean Lagacé
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, CP 6128 succ Centre-Ville, Montréal, QC H3C 3J7, Canada
Iosif Polterovich
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, CP 6128 succ Centre-Ville, Montréal, QC H3C 3J7, Canada email iossif@dms.umontreal.ca
Alessandro Savo
Affiliation:
Dipartimento SBAI, Sezione di Matematica Sapienza Università di Roma, Via Antonio Scarpa 16, 00161 Roma, Italy email alessandro.savo@sbai.uniroma1.it
Get access

Abstract

The paper is concerned with the Steklov eigenvalue problem on cuboids of arbitrary dimension. We prove a two-term asymptotic formula for the counting function of Steklov eigenvalues on cuboids in dimension $d\geqslant 3$. Apart from the standard Weyl term, we calculate explicitly the second term in the asymptotics, capturing the contribution of the 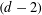$(d-2)$-dimensional facets of a cuboid. Our approach is based on lattice counting techniques. While this strategy is similar to the one used for the Dirichlet Laplacian, the Steklov case carries additional complications. In particular, it is not clear how to establish directly the completeness of the system of Steklov eigenfunctions admitting separation of variables. We prove this result using a family of auxiliary Robin boundary value problems. Moreover, the correspondence between the Steklov eigenvalues and lattice points is not exact, and hence more delicate analysis is required to obtain spectral asymptotics. Some other related results are presented, such as an isoperimetric inequality for the first Steklov eigenvalue, a concentration property of high frequency Steklov eigenfunctions and applications to spectral determination of cuboids.

MSC classification

Primary: 35P20: Asymptotic distribution of eigenvalues and eigenfunctions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 2 , 2019 , pp. 272 - 310
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Department of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K. email j.lagace@ucl.ac.uk

References

Agranovich, M. S., On a mixed Poincaré–Steklov type spectral problem in a Lipschitz domain. Russ. J. Math. Phys. 13(3) 2006, 239–244.Google Scholar
Auchmuty, G. and Cho, M., Boundary integrals and approximations of harmonic functions. Numer. Funct. Anal. Optim. 36(6) 2015, 687–703.Google Scholar
Brock, F., An isoperimetric inequality for eigenvalues of the Stekloff problem. Z. Angew. Math. Mech. 81(1) 2001, 69–71.Google Scholar
Bucur, D., Ferone, V., Nitsch, C. and Trombetti, C., Weinstock inequality in higher dimensions. Preprint, 2017, arXiv:1710.04587.Google Scholar
Girouard, A. and Polterovich, I., Spectral geometry of the Steklov problem (Survey article). J. Spectr. Theory 7(2) 2017, 321–359.Google Scholar
Gittins, K. and Larson, S., Asymptotic behaviour of cuboids optimising laplacian eigenvalues. Integral Equations Operator Theory 89(4) 2017, 607–629.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series and Products, Vol. 7, Academic Press (Burlington, MA, 2007).Google Scholar
Hlawka, E., Über Integrale auf konvexen Körpern. I. Monatsh. Math. 54 1950, 1–36.Google Scholar
Iosevich, A. and Liflyand, E., Decay of the Fourier Transform, Analytic and Geometric Aspects, Birkhäuser/Springer (Basel, 2014).Google Scholar
Ivrii, V., Spectral asymptotics for Dirichlet to Neumann operator in the domains with edges. Preprint, 2018, arXiv:1802.07524.Google Scholar
Lagacé, J. and Parnovski, L., A generalised Gauss circle problem and integrated density of states. J. Spectr. Theory 6(4) 2016, 859–879.Google Scholar
Levitin, M., Parnovski, L., Polterovich, I. and Sher, D. A., Sloshing, Steklov and corners I: asymptotics of sloshing eigenvalues. Preprint, 2017, arXiv:1709.01891.Google Scholar
Pinasco, J. P. and Rossi, J. D., Asymptotics of the spectral function for the Steklov problem in a family of sets with fractal boundaries. Appl. Math. E-Notes 5 2005, 138–146.Google Scholar
Polterovich, I. and Sher, D. A., Heat invariants of the Steklov problem. J. Geom. Anal. 25(2) 2015, 924–950.Google Scholar
Randol, B., A lattice-point problem. Trans. Amer. Math. Soc. 121 1966, 257–268.Google Scholar
Strauss, W. A., Partial Differential Equations, an Introduction, Wiley (New York, NY, 1992).Google Scholar
Tan, A., The Steklov problem on rectangles and cuboids. Preprint, 2017, arXiv:1711.00819.Google Scholar
van den Berg, M. and Gittins, K., Minimizing Dirichlet eigenvalues on cuboids of unit measure. Mathematika 63(2) 2017, 469–482.Google Scholar
Weinstock, R., Inequalities for a classical eigenvalue problem. J. Ration. Mech. Anal. 3 1954, 745–753.Google Scholar