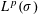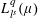Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hänninen, Timo S.
and
Verbitsky, Igor E.
2021.
On Two-Weight Norm Inequalities for Positive Dyadic Operators.
Potential Analysis,
Vol. 55,
Issue. 2,
p.
229.
Hänninen, Timo S.
Lorist, Emiel
and
Sinko, Jaakko
2025.
Weighted L → L-boundedness of commutators and paraproducts in the Bloom setting.
Journal de Mathématiques Pures et Appliquées,
Vol. 203,
Issue. ,
p.
103772.