Article contents
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
Published online by Cambridge University Press: 17 April 2018
Abstract
We generalize Skriganov’s notion of weak admissibility for lattices to include standard lattices occurring in Diophantine approximation and algebraic number theory, and we prove estimates for the number of lattice points in sets such as aligned boxes. Our result improves on Skriganov’s celebrated counting result if the box is sufficiently distorted, the lattice is not admissible, and, e.g., symplectic or orthogonal. We establish a criterion under which our error term is sharp, and we provide examples in dimensions 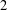 $2$ and
$2$ and 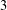 $3$ using continued fractions. We also establish a similar counting result for primitive lattice points, and apply the latter to the classical problem of Diophantine approximation with primitive points as studied by Chalk, Erdős, and others. Finally, we use o-minimality to describe large classes of sets to which our counting results apply.
$3$ using continued fractions. We also establish a similar counting result for primitive lattice points, and apply the latter to the classical problem of Diophantine approximation with primitive points as studied by Chalk, Erdős, and others. Finally, we use o-minimality to describe large classes of sets to which our counting results apply.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
References
- 3
- Cited by

