Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-11T00:02:18.161Z Has data issue: false hasContentIssue false
  • English
  • Français

All-sum sets in (0,1]—Category and measure

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

Vitaly Bergelson ,
Neil Hindman  and
Benjamin Weiss
Vitaly Bergelson
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, U.S.A.
Neil Hindman
Affiliation:
Department of Mathematics, Howard University, Washington, DC 20059, U.S.A.
Benjamin Weiss
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel.
Get access

Abstract

We provide a unified and simplified proof that for any partition of (0, 1] into sets that are measurable or have the property of Baire, one cell will contain an infinite sequence together with all of its sums (finite or infinite) without repetition. In fact any set which is large around 0 in the sense of measure or category will contain such a sequence. We show that sets with 0 as a density point have very rich structure. Call a sequence 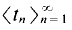and its resulting all-sums set structured provided for each 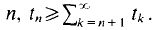We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.

MSC classification

Secondary: 28A75: Length, area, volume, other geometric measure theory
Type
Research Article
Information
Mathematika , Volume 44 , Issue 1 , June 1997 , pp. 61 - 87
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Hindman, N.. Finite sums from sequences within cells of a partition of N. J. Comb. Theory (Series A), 17 (1974), 1–11.CrossRefGoogle Scholar
2.Jørsboe, O., Meilbro, L. and Topsøe, F.. Some Vitali theorems for Lebesgue measure. Math. Scand., 48 (1981), 259–285.CrossRefGoogle Scholar
3.Menon, P. Kesava. On a class of perfect sets. Bull. Amer. Math. Soc., 54 (1948), 706–711.CrossRefGoogle Scholar
4.Oxtoby, J.. Measure and Category (Springer-Verlag, Berlin, 1971).CrossRefGoogle Scholar
5.Plewik, S. and Voigt, B.. Partitions of reals: measurable approach. J. Comb. Theory (Series A), 58 (1991), 136–140.CrossRefGoogle Scholar
6.Prömel, H. and Voigt, B.. A partition theorem for [0,1]. Proc. Amer. Math. Soc., 109 (1990), 281–285.Google Scholar