Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T17:34:23.736Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST ALL SETS OF 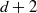$d+ 2$ POINTS ON THE 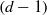$(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE

Part of: Extremal combinatorics

Published online by Cambridge University Press:  28 March 2013

Sean Eberhard
Sean Eberhard*
Affiliation:
Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, U.K. email s.eberhard@dpmms.cam.ac.uk
Get access

Abstract

We generalise an argument of Leader, Russell, and Walters to show that almost all sets of 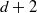$d+ 2$ points on the 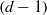$(d- 1)$-sphere 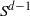${S}^{d- 1} $ are not contained in a transitive set in some 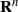${\mathbf{R} }^{n} $.

MSC classification

Secondary: 05D10: Ramsey theory
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 267 - 268
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Frankl, P. and Rödl, V., A partition property of simplices in Euclidean space. J. Amer. Math. Soc. 3 (1) (1990), 1–7.CrossRefGoogle Scholar
Johnson, F. E. A., Finite subtransitive sets. Math. Proc. Cambridge Philos. Soc. 140 (2006).CrossRefGoogle Scholar
Leader, I., Russell, P. A. and Walters, M., Transitive sets and cyclic quadrilaterals. J. Comb. 2 (3) (2011), 457–462.Google Scholar
Leader, I., Russell, P. A. and Walters, M., Transitive sets in Euclidean Ramsey theory. J. Combin. Theory Ser. A 119 (2) (2012), 382–396.CrossRefGoogle Scholar