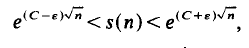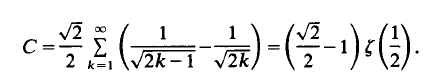Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
44.
Sander, J. W.
1995.
On the exponent average of integer sequences.
Monatshefte für Mathematik,
Vol. 120,
Issue. 2,
p.
137.
Sander, Jürgen W.
1995.
On the order of prime powers dividing ( ${}_{n}^{2n}$ ).
Acta Mathematica,
Vol. 174,
Issue. 1,
p.
85.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
71.
SHEVELEV, VLADIMIR
2007.
ON DIVISIBILITY OF ${\fontsize{9}{11}\selectfont\Big(\!\!\begin{array}{c}n-i-1\\[2pt]i-1\end{array}\!\!\Big)}$ by i.
International Journal of Number Theory,
Vol. 03,
Issue. 01,
p.
119.

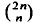 satisfies for arbitrary
satisfies for arbitrary