Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rush, J. A.
1989.
A lower bound on packing density.
Inventiones Mathematicae,
Vol. 98,
Issue. 3,
p.
499.
Mazo, J. E.
and
Odlyzko, A. M.
1990.
Lattice points in high-dimensional spheres.
Monatshefte für Mathematik,
Vol. 110,
Issue. 1,
p.
47.
Rush, J. A.
1991.
Constructive packings of cross polytopes.
Mathematika,
Vol. 38,
Issue. 2,
p.
376.
Elkies, N. D.
Odlyzko, A. M.
and
Rush, J. A.
1991.
On the packing densities of superballs and other bodies.
Inventiones Mathematicae,
Vol. 105,
Issue. 1,
p.
613.
Rush, J. A.
1993.
A bound, and a conjecture, on the maximum lattice‐packing density of a superball.
Mathematika,
Vol. 40,
Issue. 1,
p.
137.
TÖTH, Gábor FEJES
and
KUPERBERG, Wlodzimierz
1993.
Handbook of Convex Geometry.
p.
799.
Rush, J. A.
1994.
An indexed set of density bounds on lattice packings.
Geometriae Dedicata,
Vol. 53,
Issue. 2,
p.
217.
Poltyrev, Gregory
1994.
Algebraic Coding.
Vol. 781,
Issue. ,
p.
217.
1995.
Combinatorial Geometry.
p.
319.
Rush, J. A.
1995.
Compositions of sums of absolute powers.
Geometriae Dedicata,
Vol. 57,
Issue. 2,
p.
135.
Gardy, Danièle
1995.
Some results on the asymptotic behaviour of coefficients of large powers of functions.
Discrete Mathematics,
Vol. 139,
Issue. 1-3,
p.
189.
Rush, J. A.
1996.
Lattice packing of nearly-euclidean balls in spaces of even dimension.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 1,
p.
163.
Loeliger, H.-A.
1997.
Averaging bounds for lattices and linear codes.
IEEE Transactions on Information Theory,
Vol. 43,
Issue. 6,
p.
1767.
Xu, Lanju
2007.
Constructive Kissing Numbers in High-Dimensional Spaces.
Journal of Systems Science and Complexity,
Vol. 20,
Issue. 1,
p.
30.
Gaborit, Philippe
and
Zémor, Gilles
2007.
On the construction of dense lattices with a given automorphisms group.
Annales de l'Institut Fourier,
Vol. 57,
Issue. 4,
p.
1051.
Liu, Li
and
Xing, Chao Ping
2008.
Packing superballs from codes and algebraic curves.
Acta Mathematica Sinica, English Series,
Vol. 24,
Issue. 1,
p.
1.
Xing, Chaoping
2008.
Dense packings from quadratic fields and codes.
Journal of Combinatorial Theory, Series A,
Vol. 115,
Issue. 6,
p.
1021.
de A. Campello, Antonio C.
Jorge, Grasiele C.
and
Costa, Sueli I. R.
2011.
Decoding q-ary lattices in the Lee metric.
p.
220.
Sok, Lin
Sole, Patrick
and
Tchamkerten, Aslan
2013.
Lattice based codes for insertion and deletion channels.
p.
684.
Solé, Patrick
and
Belfiore, Jean-Claude
2013.
Constructive spherical codes near the Shannon bound.
Designs, Codes and Cryptography,
Vol. 66,
Issue. 1-3,
p.
17.

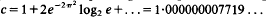 for σ = 2 (the classical sphere packing problem), worse than but surprisingly close to the Minkowski-Hlawka bound, and
for σ = 2 (the classical sphere packing problem), worse than but surprisingly close to the Minkowski-Hlawka bound, and 