Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:54:21.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Arakelyan's theorem and relations between two harmonic functions

Part of: Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  26 February 2010

J. M. Anderson  and
A. Hinkkanen
J. M. Anderson
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K.
A. Hinkkanen
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 West Green Street, Urbana, IL 61801, U.S.A.
Get access

Abstract

It is shown that, if h and k are harmonic in ℝ2 and there exists a positive constant c so that

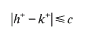
in ℝ2, where h+ = max {h, 0}, then it need not follow that h - k is identically a constant. The necessary counterexample is obtained by applying Arakelyan's theorem on approximation by an entire function in certain regions in ℝ2.

MSC classification

Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Mathematika , Volume 48 , Issue 1-2 , December 2001 , pp. 301 - 304
Copyright
Copyright © University College London 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Gaier, D.. Lectures on Complex Approximation (Birkhauser, 1987).CrossRefGoogle Scholar
2.Lewis, J. L.. Picard's theorem and Rickman's theorem by way of Harnack's inequality. Proc. Amer. Math. Soc. 122 (1994), 199–206.Google Scholar
3.Llorente, J. L.. Private communication.Google Scholar
4.Ransford, T. J.. Potential Theory in the Complex Plane. London Mathematical Society Student Texts, 28 (Cambridge, 1995).CrossRefGoogle Scholar
5.Rickman, S.. On the number of omitted values of entire quasi-regular mappings. J. d'Analyse Math. 37(1980), 100–117.CrossRefGoogle Scholar